
【题目】对于四个数“![]() ,
,![]() ,
,![]() ,
,![]() ”及四种运算“
”及四种运算“![]() ,
,![]() ,
,![]() ,
,![]() ”,列算式解答:
”,列算式解答:
(1)求这四个数的和;
(2)在这四个数中选出两个数,按要求进行下列计算,使得:
①两数差的结果最小;
②两数积的结果最大;
(3)在这四个数中选出三个数,在四种运算中选出两种,组成一个算式,使运算结果等于没选的那个数.
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案科目:初中数学 来源: 题型:
【题目】为积极响应政府提出的“绿色发展·低碳出行”号召,某社区决定购置一批共享单车,经市场调查得知,购买3量男式单车与4辆女式单车费用相同,购买5辆男式单车与4辆女式单车共需16000元.
(1)求男式单车和女式单车的单价;
(2)该社区要求男式单比女式单车多4辆,两种单车至少需要22辆,购置两种单车的费用不超过50000元,该社区有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,钝角△ABC中,AB=AC,BC=2![]() ,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
,O是边AB上一点,以O为圆心,OB为半径作⊙O,交边AB于点D,交边BC于点E,过E作⊙O的切线交边AC于点F.
(1)求证:EF⊥AC.
(2)连结DF,若∠ABC=30°,且DF∥BC,求⊙O的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表
最受欢迎兴趣班调查问卷 | 统计表 | |||||
选项 | 兴趣班 | 请选择 | 兴趣班 | 频数 | 频率 | |
A | 绘画 | A | 0.35 | |||
B | 音乐 | B | 18 | 0.30 | ||
C | 舞蹈 | C | 15 |
| ||
D | 跆拳道 | D | 6 | |||
你好!请选择一个(只能选一个)你最喜欢的兴趣班,在其后空格内打“√”,谢谢你的合作. |
| 1 | ||||
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)根据调查结果,请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数;
(3)王姝和李要选择参加兴趣班,若他们每人从A、B、C、D四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有专家指出:人为型空气污染(如汽车尾气排放等)是雾霾天气的重要成因.某校为倡议“每人少开一天车,共建绿色家园”,想了解学生上学的交通方式.九年级(8)班的5名同学联合设计了一份调查问卷.对该校部分学生进行了随机调查.按A(骑自行车)、B(乘公交车)、C(步行)、D(乘私家车)、E(其他方式)设置选项,要求被调查同学从中单选.并将调查结果绘制成条形统计图1和扇形统计图2,根据以上信息,解答下列问题:
(1)本次接受调查的总人数是 人,扇形统计图中“骑自行车”所在扇形的圆心角度数是 度,请补全条形统计图;
(2)已知这5名学生中有2名女同学,要从这5名学生中任选两名同学汇报调查结果.请用列表法或画树状图的方法,求出恰好选出1名男生和1名女生的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某游乐园有一个直径为16米的圆形喷水池,喷水池的周边有一圈喷水头,喷出的水柱为抛物线,在距水池中心3米处达到最高,高度为5米,且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合.如图所示,以水平方向为x轴,喷水池中心为原点建立直角坐标系.
(1)求水柱所在抛物线(第一象限部分)的函数表达式;
(2)王师傅在喷水池内维修设备期间,喷水管意外喷水,为了不被淋湿,身高1.8米的王师傅站立时必须在离水池中心多少米以内?
(3)经检修评估,游乐园决定对喷水设施做如下设计改进:在喷出水柱的形状不变的前提下,把水池的直径扩大到32米,各方向喷出的水柱仍在喷水池中心保留的原装饰物(高度不变)处汇合,请探究扩建改造后喷水池水柱的最大高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
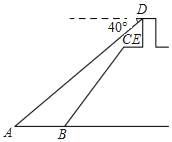
【题目】如图,小明站在江边某瞭望台DE的顶端D处,测得江面上的渔船A的俯角为40°.若瞭望台DE垂直于江面,它的高度为3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡长BC=10米.
(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,cot40°≈1.19)
(1)求瞭望台DE的顶端D到江面AB的距离;
(2)求渔船A到迎水坡BC的底端B的距离.(结果保留一位小数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个边长分别为![]() 和
和![]() 的正方形如图放置(图1),其未叠合部分(阴影)面积为
的正方形如图放置(图1),其未叠合部分(阴影)面积为![]() ;若再在图1中大正方形的右下角摆放一个边长为
;若再在图1中大正方形的右下角摆放一个边长为![]() 的小正方形(如图2),两个小正方形叠合部分(阴影)面积为
的小正方形(如图2),两个小正方形叠合部分(阴影)面积为![]() .
.



(1)用含![]() 、
、![]() 的代数式分别表示
的代数式分别表示![]() 、
、![]() ;
;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)当![]() 时,求出图3中阴影部分的面积
时,求出图3中阴影部分的面积![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com