
【题目】某市少年宫为小学生开设了绘画、音乐、舞蹈和跆拳道四类兴趣班,为了解学生对这四类兴趣班的喜爱情况,对学生进行了随机问卷调查(问卷调查表如图所示),将调查结果整理后绘制了一幅不完整的统计表
最受欢迎兴趣班调查问卷 | 统计表 | |||||
选项 | 兴趣班 | 请选择 | 兴趣班 | 频数 | 频率 | |
A | 绘画 | A | 0.35 | |||
B | 音乐 | B | 18 | 0.30 | ||
C | 舞蹈 | C | 15 |
| ||
D | 跆拳道 | D | 6 | |||
你好!请选择一个(只能选一个)你最喜欢的兴趣班,在其后空格内打“√”,谢谢你的合作. |
| 1 | ||||
请你根据统计表中提供的信息回答下列问题:
(1)统计表中的![]() ,
,![]() ;
;
(2)根据调查结果,请你估计该市2000名小学生中最喜欢“绘画”兴趣的人数;
(3)王姝和李要选择参加兴趣班,若他们每人从A、B、C、D四类兴趣班中随机选取一类,请用画树状图或列表格的方法,求两人恰好选中同一类的概率.
【答案】(1)a=60,b=0.25;(2)最喜欢绘画的人数为700人;(3)![]()
【解析】
(1)用B选项人数除以它所占的百分比得到a的值,然后用C选项的频数除以a得到b的值;
(2)用2000乘以样本中最喜欢“绘画”兴趣班的人数所占的百分比即可;
(3)画树状图展示所有16种等可能的结果数,找出恰好选中同一类的结果数,然后根据概率公式求解,
解:(1)调查的总人数为18÷0.3=60(人),即a=60,
b=15÷60=0.25;
故答案为:60,0.25;
(2)2000×0.35=700(人),
答:最喜欢绘画的人数为700人.
(3)如下表:
李要 王姝 | A | B | C | D |
A | AA | AB | AC | AD |
B | AB | BB | CB | DB |
C | AC | BC | CC | DC |
D | AD | BD | CD | DD |
由上表得,共有16种等可能的情况,其中两人恰好选中同一类的情况有4种,
所以两人恰好选中同一类的概率是![]() .
.


 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=6,对角线AC和BD相交于点O,E是AB所在直线上一点(不与点B重合),将线段OE绕点E顺时针旋转90°得到EF.
(1)如图1,当点E和点A重合时,连接BF,直接写出BF的长为 ;
(2)如图2,点E在线段AB上,且AE=1,连接BF,求BF的长;
(3)若DG:AG=2:1,连接CF,H是CF的中点,是否存在点E使△GEH是以EG为直角边的直角三角形?若存在,请直接写出EB的长;若不存在,试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于
轴交于![]() 点,抛物线顶点为
点,抛物线顶点为![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() 点.
点.
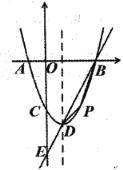
(1)求抛物线函数表达式;
(2)若点![]() 是位于直线
是位于直线![]() 下方抛物线上的一动点,以
下方抛物线上的一动点,以![]() 、
、![]() 为相邻的两边作平行四边形
为相邻的两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时平行四边形
的面积最大时,求此时平行四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某建筑物的顶部有一块标识牌 CD,小明在斜坡上 B 处测得标识牌顶部C 的仰角为 45°, 沿斜坡走下来在地面 A 处测得标识牌底部 D 的仰角为 60°,已知斜坡 AB 的坡角为 30°,AB=AE=10 米.则标识牌 CD 的高度是( )米.
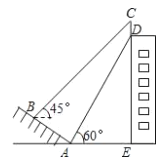
A.15-5![]() B.20-10
B.20-10![]() C.10-5
C.10-5![]() D.5
D.5![]() -5
-5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,△ABC和△DEC是两个全等的直角三角形纸片,其中∠ACB=∠DCE=90°,∠B=∠E=30°,AB=DE=4.
解决问题:
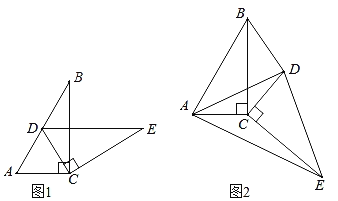
(1)如图1,智慧小组将△DEC绕点C顺时针旋转,发现当点D恰好落在AB边上时,DE∥AC,请你帮他们证明这个结论;
(2)缜密小组在智慧小组的基础上继续探究,当△DEC绕点C继续旋转到如图2所示的位置时,连接AE、AD、BD,他们提出S△BDC=S△AEC,请你帮他们验证这一结论是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y=![]() 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.
(1)求反比例函数和一次函数的解析式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于四个数“![]() ,
,![]() ,
,![]() ,
,![]() ”及四种运算“
”及四种运算“![]() ,
,![]() ,
,![]() ,
,![]() ”,列算式解答:
”,列算式解答:
(1)求这四个数的和;
(2)在这四个数中选出两个数,按要求进行下列计算,使得:
①两数差的结果最小;
②两数积的结果最大;
(3)在这四个数中选出三个数,在四种运算中选出两种,组成一个算式,使运算结果等于没选的那个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
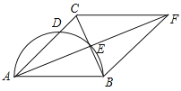
【题目】如图,在△ABC中,AB=AC,以AB为直径的半圆交AC于点D,交BC于点E,延长AE至点F,使EF=AE,连接FB、FC.
(1)求证:四边形ABFC是菱形;
(2)若AD=![]() ,BE=1,求半圆的面积.
,BE=1,求半圆的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
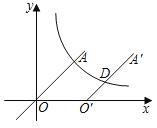
【题目】如图,正比例函数y=x的图象与反比例函数y=![]() 的图象在第一象限交于点A,将线段OA沿x轴向右平移3个单位长度得到线段O'A',其中点A与点A'对应,若O'A'的中点D恰好也在该反比例函数图象上,则k的值为_____.
的图象在第一象限交于点A,将线段OA沿x轴向右平移3个单位长度得到线段O'A',其中点A与点A'对应,若O'A'的中点D恰好也在该反比例函数图象上,则k的值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com