
ЁОЬтФПЁПЮЪЬтЧщОГЃК
Ъ§бЇЛюЖЏПЮЩЯЃЌРЯЪІШУЭЌбЇУЧвдЁАШ§НЧаЮЕФа§зЊЁБЮЊжїЬтПЊеЙЪ§бЇЛюЖЏЃЌЁїABCКЭЁїDECЪЧСНИіШЋЕШЕФжБНЧШ§НЧаЮжНЦЌЃЌЦфжаЁЯACBЃНЁЯDCEЃН90ЁуЃЌЁЯBЃНЁЯEЃН30ЁуЃЌABЃНDEЃН4ЃЎ
НтОіЮЪЬтЃК
ЃЈ1ЃЉШчЭМ1ЃЌжЧЛлаЁзщНЋЁїDECШЦЕуCЫГЪБеыа§зЊЃЌЗЂЯжЕБЕуDЧЁКУТфдкABБпЩЯЪБЃЌDEЁЮACЃЌЧыФуАяЫћУЧжЄУїетИіНсТлЃЛ
ЃЈ2ЃЉчЧУмаЁзщдкжЧЛлаЁзщЕФЛљДЁЩЯМЬајЬНОПЃЌЕБЁїDECШЦЕуCМЬаја§зЊЕНШчЭМ2ЫљЪОЕФЮЛжУЪБЃЌСЌНгAEЁЂADЁЂBDЃЌЫћУЧЬсГіSЁїBDCЃНSЁїAECЃЌЧыФуАяЫћУЧбщжЄетвЛНсТлЪЧЗёе§ШЗЃЌВЂЫЕУїРэгЩЃЎ
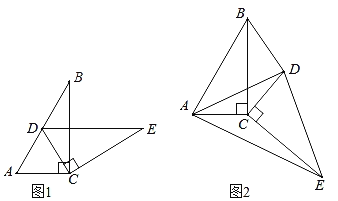
ЁОД№АИЁПЃЈ1ЃЉжЄУїМћНтЮіЃЛЃЈ2ЃЉе§ШЗЃЌРэгЩМћНтЮі
ЁОНтЮіЁП
ЃЈ1ЃЉШчЭМ1жаЃЌИљОна§зЊЕФаджЪПЩЕУACЃНCDЃЌШЛКѓЧѓГіЁїACDЪЧЕШБпШ§НЧаЮЃЌИљОнЕШБпШ§НЧаЮЕФаджЪПЩЕУЁЯACDЃН60ЁуЃЌШЛКѓИљОнФкДэНЧЯрЕШЃЌСНжБЯпЦНааНјааНтД№ЃЛ
ЃЈ2ЃЉШчЭМ2жаЃЌзїDMЁЭBCгкMЃЌANЁЭECНЛECЕФбгГЄЯпгкNЃЎИљОна§зЊЕФаджЪПЩЕУBCЃНCEЃЌACЃНCDЃЌдйЧѓГіЁЯACNЃНЁЯDCMЃЌШЛКѓРћгУЁАНЧНЧБпЁБжЄУїЁїACNКЭЁїDCMШЋЕШЃЌИљОнШЋЕШШ§НЧаЮЖдгІБпЯрЕШПЩЕУANЃНDMЃЌШЛКѓРћгУЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШжЄУїЃЎ
НтЃКЃЈ1ЃЉШчЭМ1жаЃЌЁпЁїDECШЦЕуCа§зЊЕуDЧЁКУТфдкABБпЩЯЃЌ
ЁрACЃНCDЃЌ
ЁпЁЯBACЃН90ЁуЉЁЯBЃН90ЁуЉ30ЁуЃН60ЁуЃЌ
ЁрЁїACDЪЧЕШБпШ§НЧаЮЃЌ
ЁрЁЯACDЃН60ЁуЃЌ
гжЁпЁЯCDEЃНЁЯBACЃН60ЁуЃЌ
ЁрЁЯACDЃНЁЯCDEЃЌ
ЁрDEЁЮACЃЛ
ЃЈ2ЃЉНсТле§ШЗЃЌ
РэгЩШчЯТЃКШчЭМ2жаЃЌзїDMЁЭBCгкMЃЌANЁЭECНЛECЕФбгГЄЯпгкNЃЎ

ЁпЁїDECЪЧгЩЁїABCШЦЕуCа§зЊЕУЕНЃЌ
ЁрBCЃНCEЃЌACЃНCDЃЌ
ЁпЁЯACNЃЋЁЯBCNЃН90ЁуЃЌЁЯDCMЃЋЁЯBCNЃН180ЁуЉ90ЁуЃН90ЁуЃЌ
ЁрЁЯACNЃНЁЯDCMЃЌ
дкЁїACNКЭЁїDCMжаЃЌ
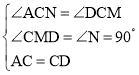 ЃЌ
ЃЌ
ЁрЁїACNЁеЁїDCMЃЈAASЃЉЃЌ
ЁрANЃНDMЃЌ
ЁрЁїBDCЕФУцЛ§КЭЁїAECЕФУцЛ§ЯрЕШЃЈЕШЕзЕШИпЕФШ§НЧаЮЕФУцЛ§ЯрЕШЃЉЃЌ
МДSЁїBDCЃНSЁїAECЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФЯЖДЭЅДѓЧХЪЧФЯвцИпЫйЙЋТЗЩЯЕФживЊЧХСКЃЌаЁЗМЭЌбЇдкаЃЭтЪЕМљЛюЖЏжаЖдДЫПЊеЙВтСПЛюЖЏЃЎШчЭМЃЌдкЧХЭтвЛЕуAВтЕУДѓЧХжїМмгыЫЎУцЕФНЛЛуЕуCЕФИЉНЧЮЊІСЃЌДѓЧХжїМмЕФЖЅЖЫDЕФбіНЧЮЊІТЃЌвбжЊВтСПЕугыДѓЧХжїМмЕФЫЎЦНОрРыABЃНaЃЌдђДЫЪБДѓЧХжїМмЖЅЖЫРыЫЎУцЕФИпCDЮЊ( )
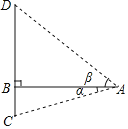
A.asinІС+asinІТB.acosІС+acosІТC.atanІС+atanІТD.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкОиаЮ![]() жаЃЌЗжБ№вд
жаЃЌЗжБ№вд![]() ЃЌ
ЃЌ![]() ЫљдкжБЯпЮЊ
ЫљдкжБЯпЮЊ![]() жсЃЌ
жсЃЌ![]() жсЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЎ
жсЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЎ![]() ЪЧ
ЪЧ![]() БпЩЯвЛИіЖЏЕуЃЈВЛгы
БпЩЯвЛИіЖЏЕуЃЈВЛгы![]() ЃЌ
ЃЌ![]() жиКЯЃЉЃЌЙ§Еу
жиКЯЃЉЃЌЙ§Еу![]() ЕФЗДБШР§КЏЪ§
ЕФЗДБШР§КЏЪ§![]()
![]() ЕФЭМЯѓгыБп
ЕФЭМЯѓгыБп![]() НЛгкЕу
НЛгкЕу![]() ЃЌвбжЊ
ЃЌвбжЊ![]() ЃЌ
ЃЌ![]() ЃЌНЋ
ЃЌНЋ![]() би
би![]() елЕўЃЌЕу
елЕўЃЌЕу![]() ЧЁКУТфдкБп
ЧЁКУТфдкБп![]() ЩЯЕФЕу
ЩЯЕФЕу![]() ДІЃЌдђ
ДІЃЌдђ![]() ________ЃЎ
________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЖлНЧЁїABCжаЃЌAB=ACЃЌBC=2![]() ЃЌOЪЧБпABЩЯвЛЕуЃЌвдOЮЊдВаФЃЌOBЮЊАыОЖзїЁбOЃЌНЛБпABгкЕуDЃЌНЛБпBCгкЕуEЃЌЙ§EзїЁбOЕФЧаЯпНЛБпACгкЕуFЃЎ
ЃЌOЪЧБпABЩЯвЛЕуЃЌвдOЮЊдВаФЃЌOBЮЊАыОЖзїЁбOЃЌНЛБпABгкЕуDЃЌНЛБпBCгкЕуEЃЌЙ§EзїЁбOЕФЧаЯпНЛБпACгкЕуFЃЎ
ЃЈ1ЃЉЧѓжЄЃКEFЁЭACЃЎ
ЃЈ2ЃЉСЌНсDFЃЌШєЁЯABC=30ЁуЃЌЧвDFЁЮBCЃЌЧѓЁбOЕФАыОЖГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕуA1ЕФзјБъЮЊ(0ЃЌ1)ЃЌЕуA2дкxжсЕФе§АыжсЩЯЃЌЧвЁЯA1A2OЃН30ЁуЃЌЙ§ЕуA2зїA2A3ЁЭA1A2ЃЌНЛyжсгкЕуA3ЃЛЙ§ЕуA3зїA3A4ЁЭA2A3ЃЌНЛxжсгкЕуA4ЃЛЙ§ЕуA4зїA4A5ЁЭA3A4ЃЌНЛyжсгкЕуA5ЃЛЁЁЃЛАДДЫЙцТЩНјааЯТШЅЃЌдђЕуA2021ЕФзјБъЮЊЃЈ ЃЉ
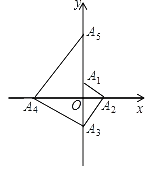
A.(0ЃЌ31011)B.(Љ31011ЃЌ0)C.(0ЃЌ31010)D.(Љ31010ЃЌ0)
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЩйФъЙЌЮЊаЁбЇЩњПЊЩшСЫЛцЛЁЂвєРжЁЂЮшЕИКЭѕЬШЕРЫФРраЫШЄАрЃЌЮЊСЫНтбЇЩњЖдетЫФРраЫШЄАрЕФЯВАЎЧщПіЃЌЖдбЇЩњНјааСЫЫцЛњЮЪОэЕїВщЃЈЮЪОэЕїВщБэШчЭМЫљЪОЃЉЃЌНЋЕїВщНсЙћећРэКѓЛцжЦСЫвЛЗљВЛЭъећЕФЭГМЦБэ
зюЪмЛЖгаЫШЄАрЕїВщЮЪОэ | ЭГМЦБэ | |||||
бЁЯю | аЫШЄАр | ЧыбЁдё | аЫШЄАр | ЦЕЪ§ | ЦЕТЪ | |
A | ЛцЛ | A | 0.35 | |||
B | вєРж | B | 18 | 0.30 | ||
C | ЮшЕИ | C | 15 |
| ||
D | ѕЬШЕР | D | 6 | |||
ФуКУЃЁЧыбЁдёвЛИіЃЈжЛФмбЁвЛИіЃЉФузюЯВЛЖЕФаЫШЄАрЃЌдкЦфКѓПеИёФкДђЁАЁЬЁБЃЌаЛаЛФуЕФКЯзї. |
| 1 | ||||
ЧыФуИљОнЭГМЦБэжаЬсЙЉЕФаХЯЂЛиД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉЭГМЦБэжаЕФ![]() ЃЌ
ЃЌ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉИљОнЕїВщНсЙћЃЌЧыФуЙРМЦИУЪа2000УћаЁбЇЩњжазюЯВЛЖЁАЛцЛЁБаЫШЄЕФШЫЪ§ЃЛ
ЃЈ3ЃЉЭѕцКЭРювЊбЁдёВЮМгаЫШЄАрЃЌШєЫћУЧУПШЫДгAЁЂBЁЂCЁЂDЫФРраЫШЄАржаЫцЛњбЁШЁвЛРрЃЌЧыгУЛЪїзДЭМЛђСаБэИёЕФЗНЗЈЃЌЧѓСНШЫЧЁКУбЁжаЭЌвЛРрЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгазЈМвжИГіЃКШЫЮЊаЭПеЦјЮлШОЃЈШчЦћГЕЮВЦјХХЗХЕШЃЉЪЧЮэіВЬьЦјЕФживЊГЩвђЃЎФГаЃЮЊГЋвщЁАУПШЫЩйПЊвЛЬьГЕЃЌЙВНЈТЬЩЋМвдАЁБЃЌЯыСЫНтбЇЩњЩЯбЇЕФНЛЭЈЗНЪНЃЎОХФъМЖЃЈ8ЃЉАрЕФ5УћЭЌбЇСЊКЯЩшМЦСЫвЛЗнЕїВщЮЪОэЃЎЖдИУаЃВПЗжбЇЩњНјааСЫЫцЛњЕїВщЃЎАДAЃЈЦяздааГЕЃЉЁЂBЃЈГЫЙЋНЛГЕЃЉЁЂCЃЈВНааЃЉЁЂDЃЈГЫЫНМвГЕЃЉЁЂEЃЈЦфЫћЗНЪНЃЉЩшжУбЁЯюЃЌвЊЧѓБЛЕїВщЭЌбЇДгжаЕЅбЁЃЎВЂНЋЕїВщНсЙћЛцжЦГЩЬѕаЮЭГМЦЭМ1КЭЩШаЮЭГМЦЭМ2ЃЌИљОнвдЩЯаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮНгЪмЕїВщЕФзмШЫЪ§ЪЧЁЁ ЁЁШЫЃЌЩШаЮЭГМЦЭМжаЁАЦяздааГЕЁБЫљдкЩШаЮЕФдВаФНЧЖШЪ§ЪЧЁЁ ЁЁЖШЃЌЧыВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉвбжЊет5УћбЇЩњжага2УћХЎЭЌбЇЃЌвЊДгет5УћбЇЩњжаШЮбЁСНУћЭЌбЇЛуБЈЕїВщНсЙћЃЎЧыгУСаБэЗЈЛђЛЪїзДЭМЕФЗНЗЈЃЌЧѓГіЧЁКУбЁГі1УћФаЩњКЭ1УћХЎЩњЕФИХТЪЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩфЛїдЫЖЏдБдкбЕСЗжаЩфЛїСЫ10ДЮЃЌГЩМЈШчЭМЃЌЯТСаНсТле§ШЗЕФЪЧЃЈ ЃЉ
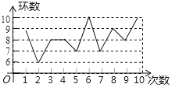
A.ЦНОљЪ§ЪЧ8B.жкЪ§ЪЧ8 C.жаЮЛЪ§ЪЧ9 D.ЗНВюЪЧ1
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
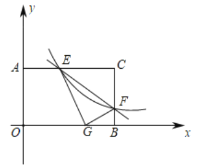
ЁОЬтФПЁПШчЭМЃЌвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсИКАыжсНЛгкЕуAЃЈ-1ЃЌ0ЃЉЃЌгыyжсе§АыжсНЛгыЕуBЃЌЖЅЕуЮЊPЃЌЧвOB=3OAЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓОЙ§AЁЂBЃЎ
ЕФЭМЯѓгыxжсИКАыжсНЛгкЕуAЃЈ-1ЃЌ0ЃЉЃЌгыyжсе§АыжсНЛгыЕуBЃЌЖЅЕуЮЊPЃЌЧвOB=3OAЃЌвЛДЮКЏЪ§y=kx+bЕФЭМЯѓОЙ§AЁЂBЃЎ
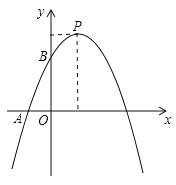
(1) ЧѓвЛДЮКЏЪ§НтЮіЪНЃЛ
(2)ЧѓЖЅЕуPЕФзјБъЃЛ
(3)ЦНвЦжБЯпABЪЙЦфЙ§ЕуPЃЌШчЙћЕуЃЭдкЦНвЦКѓЕФжБЯпЩЯЃЌЧв![]() ЃЌЧѓЕуMзјБъЃЛ
ЃЌЧѓЕуMзјБъЃЛ
(4)ЩшХзЮяЯпЕФЖдГЦжсНЛxжсгыЕуEЃЌСЊНсAPНЛyжсгыЕуDЃЌШєЕуQЁЂNЗжБ№ЮЊСНЯпЖЮPEЁЂPDЩЯЕФЖЏЕуЃЌСЊНсQDЁЂQNЃЌЧыжБНгаДГіQD+QNЕФзюаЁжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com