
【题目】在矩形![]() 中,分别以
中,分别以![]() ,
,![]() 所在直线为
所在直线为![]() 轴,
轴,![]() 轴,建立如图所示的平面直角坐标系.
轴,建立如图所示的平面直角坐标系.![]() 是
是![]() 边上一个动点(不与
边上一个动点(不与![]() ,
,![]() 重合),过点
重合),过点![]() 的反比例函数
的反比例函数![]()
![]() 的图象与边
的图象与边![]() 交于点
交于点![]() ,已知
,已知![]() ,
,![]() ,将
,将![]() 沿
沿![]() 折叠,点
折叠,点![]() 恰好落在边
恰好落在边![]() 上的点
上的点![]() 处,则
处,则![]() ________.
________.
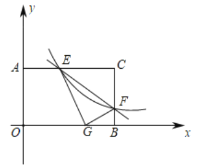
【答案】![]()
【解析】
证明Rt△MEG∽Rt△BGF,则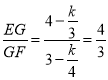 ,而EM:GB=EG:GF=4:3,求出GB,在Rt△GBF中,利用勾股定理即可求解.
,而EM:GB=EG:GF=4:3,求出GB,在Rt△GBF中,利用勾股定理即可求解.
解:如图,过点E作EM⊥x轴于点M,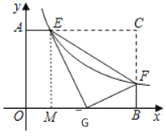
∵将△CEF沿EF对折后,C点恰好落在OB上的G点处,
∴∠EGF=∠C=90°,EC=EG,CF=GF,
∴∠MGE+∠FGB=90°,
而EM⊥OB,
∴∠MGE+∠MEG=90°,
∴∠MEG=∠FGB,
∴Rt△MEG∽Rt△BGF;
又∵EC=AC-AE=4-![]() ,CF=BC-BF=3-
,CF=BC-BF=3-![]() ,
,
∴EG=4-![]() ,GF=3-
,GF=3-![]() ,
,
∴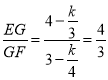 .
.
∵EM:GB=EG:GF=4:3,而EM=3,
∴GB=![]() ,
,
在Rt△GBF中,GF2=GB2+BF2,即(3-![]() )2=(
)2=(![]() )2+(
)2+(![]() )2,
)2,
解得k=![]() ,
,
故答案为![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】定义:有一组邻边相等且对角互补的四边形叫做等补四边形.
理解:
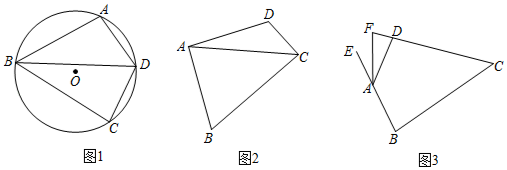
![]() 如图1,点
如图1,点![]() 在
在![]() 上,
上,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,连接
,连接![]() 求证:四边形
求证:四边形![]() 是等补四边形;
是等补四边形;
探究:
![]() 如图2,在等补四边形
如图2,在等补四边形![]() 中
中![]() 连接
连接![]() 是否平分
是否平分![]() 请说明理由.
请说明理由.
运用:
![]() 如图3,在等补四边形
如图3,在等补四边形![]() 中,
中,![]() ,其外角
,其外角![]() 的平分线交
的平分线交![]() 的延长线于点
的延长线于点![]() 求
求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
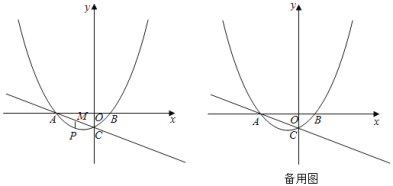
【题目】如图,抛物线![]() 交x轴于A,B两点,交y轴于点C.直线
交x轴于A,B两点,交y轴于点C.直线![]() 经过点A,C.
经过点A,C.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当![]() 是直角三角形时,求点P的坐标;
是直角三角形时,求点P的坐标;
②作点B关于点C的对称点![]() ,则平面内存在直线l,使点M,B,
,则平面内存在直线l,使点M,B,![]() 到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线
到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线![]() 的解析式.(k,b可用含m的式子表示)
的解析式.(k,b可用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解社区居民公共卫生意识情况,社区网格员随机抽查了若干居民开展“抗击疫情相关规定”有奖问答活动,并用得到的数据绘制了条形统计图.
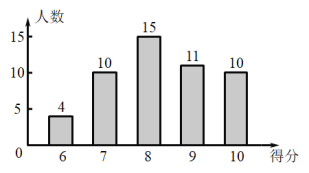
请根据图中信息,解答下列问题:
(1)本次抽查的居民人数;
(2)本次抽查获取的样本数据的平均数、众数和中位数;
(3)社区决定对本区500户居民开展这项有奖间答活动(每户抽1人),得10分者设为“一等奖”.请你根据调查结果,帮社区工作人员估计需准备多少份“一等奖”奖品?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年春节,一场突如其来的新型冠状肺炎病毒疫情在武汉突发,为响应党中央号召,在“支援武汉,防控疫情”的过程中,某省计划组织1441名医护人员的“援汉”团队前往武汉进行支援,经过研究,决定租用当地租车公司一共62辆![]() 、
、![]() 两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
两种型号客车作为交通工具,下表是租车公司提供给学校有关两种型号客车的载客量和租金信息:
型号 | 载客量 | 租金单价 |
| 30人 | 380元 |
| 20人 | 280元 |
注:载客量指的是每辆客车最多可载医护人员的人数.
(1)设租用![]() 型号客车
型号客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元,求
元,求![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
(2)若要使租车总费用不超过19900元,一共有几种租车方案?哪种租车方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于
轴交于![]() 点,抛物线顶点为
点,抛物线顶点为![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() 点.
点.
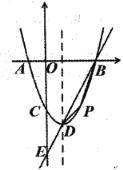
(1)求抛物线函数表达式;
(2)若点![]() 是位于直线
是位于直线![]() 下方抛物线上的一动点,以
下方抛物线上的一动点,以![]() 、
、![]() 为相邻的两边作平行四边形
为相邻的两边作平行四边形![]() ,当平行四边形
,当平行四边形![]() 的面积最大时,求此时平行四边形
的面积最大时,求此时平行四边形![]() 的面积
的面积![]() 及点
及点![]() 的坐标;
的坐标;
(3)在线段![]() 上是否存在点
上是否存在点![]() ,使得
,使得![]() ?若存在,求出点
?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设点A(x1,y1)和点B(x2,y2)是反比例函数y=![]() 图象上的两点,当x1<x2<0时,y1>y2,则一次函数y=-2x+k的图象不经过的象限是( )
图象上的两点,当x1<x2<0时,y1>y2,则一次函数y=-2x+k的图象不经过的象限是( )
A.第一象限B.第二象限C.第三象限D.第四象限
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题情境:
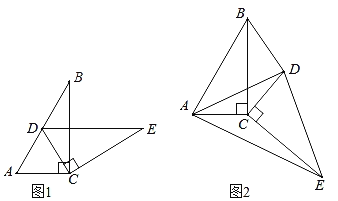
数学活动课上,老师让同学们以“三角形的旋转”为主题开展数学活动,△ABC和△DEC是两个全等的直角三角形纸片,其中∠ACB=∠DCE=90°,∠B=∠E=30°,AB=DE=4.
解决问题:
(1)如图1,智慧小组将△DEC绕点C顺时针旋转,发现当点D恰好落在AB边上时,DE∥AC,请你帮他们证明这个结论;
(2)缜密小组在智慧小组的基础上继续探究,当△DEC绕点C继续旋转到如图2所示的位置时,连接AE、AD、BD,他们提出S△BDC=S△AEC,请你帮他们验证这一结论是否正确,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
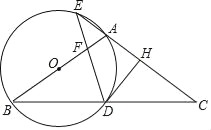
【题目】如图,在△ABC中,AB=AC,以AB为直径作圆O,分别交BC于点D,交CA的延长线于点E,过点D作DH⊥AC于点H,连接DE交线段OA于点F.
(1)求证:DH是圆O的切线;
(2)若A为EH的中点,求![]() 的值;
的值;
(3)若EA=EF=1,求圆O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com