
 如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.
如图,抛物线y=-$\frac{5}{4}$x2+bx+c与y轴交于点A(0,1),过点A的直线与抛物线交于另一点B(3,$\frac{5}{2}$),过点B作BC⊥x轴,垂足为C.点P是x轴正半轴上的一动点,过点P作PN⊥x轴,交直线AB于点M,交抛物线于点N,设OP的长度为m.分析 (1)直接把AB两点的坐标代入抛物线y=-$\frac{5}{4}$x2+bx+c,求出b、c的值即可得出抛物线的解析式;
(2)利用待定系数法求出直线AB的解析式,再根据P、M两点的坐标即可得出PM的长;
(3)根据点N在抛物线上可知N(m,-$\frac{5}{4}$m2+$\frac{17}{4}$m+1),再由MN∥BC可知当MN=BC时,四边形BCMN为平行四边形,分点P在线段OC上与点P在线段OC的延长线上两种情况进行讨论即可.
解答 解:(1)∵抛物线y=-$\frac{5}{4}$x2+bx+c经过A(0,1)和点B(3,$\frac{5}{2}$),
∴$\left\{\begin{array}{l}c=1\\-\frac{5}{4}×9+3b+1=\frac{5}{2}\end{array}\right.$,
∴$\left\{\begin{array}{l}c=1\\ b=\frac{17}{4}\end{array}\right.$,
∴抛物线的解析式为y=-$\frac{5}{4}$x2+$\frac{17}{4}$x+1;
(2)设直线AB的解析式为y=kx+b(k≠0),
∵A(0,1),B(3,$\frac{5}{2}$),
∴$\left\{\begin{array}{l}1=b\\ \frac{5}{2}=3k+b\end{array}\right.$,
∴直线AB的解析式为y=$\frac{1}{2}$x+1,
∵PN⊥x轴,交直线AB于点M,交抛物线于点N,OP=m,
∴P(m,0),M(m,$\frac{1}{2}$m+1),
∴PM=$\frac{1}{2}$m+1;
(3)由题意可得:N(m,-$\frac{5}{4}$m2+$\frac{17}{4}$m+1),
∵MN∥BC,
∴当MN=BC时,四边形BCMN为平行四边形,
当点P在线段OC上时,MN=-$\frac{5}{4}$m2+$\frac{15}{4}$m,
又∵BC=$\frac{5}{2}$,
∴-$\frac{5}{4}$m2+$\frac{15}{4}$m=$\frac{5}{2}$,
解得m1=1,m2=2;
当点P在线段OC的延长线上时,MN=$\frac{5}{4}$m2-$\frac{15}{4}$m,
∴$\frac{5}{4}$m2-$\frac{15}{4}$m=$\frac{5}{2}$,
解得 m1=$\frac{3-\sqrt{17}}{2}$(不合题意,舍去),m2=$\frac{3+\sqrt{17}}{2}$,
综上所述,当m的值为1或2或$\frac{3+\sqrt{17}}{2}$时,以B、C、M、N为顶点的四边形为平行四边形.
点评 本题考查的是二次函数综合题,涉及到利用待定系数法求二次函数的解析式,平行四边形的判定与性质等知识,在解答(3)时要注意进行分类讨论.


科目:初中数学 来源: 题型:选择题
| A. | 159.06 | B. | 50.36 | C. | 1590.6 | D. | 503.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
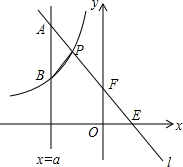 如图,直线y=kx+b与坐标轴分别交于点E、F,与双曲线y=-$\frac{m}{x}$(x<0)交于点P(-1,4),且F是PE的中点.
如图,直线y=kx+b与坐标轴分别交于点E、F,与双曲线y=-$\frac{m}{x}$(x<0)交于点P(-1,4),且F是PE的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
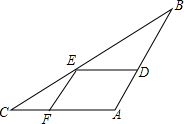 如图,△ABC中,DE∥AC,EF∥AB,∠BED=∠CEF,
如图,△ABC中,DE∥AC,EF∥AB,∠BED=∠CEF,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
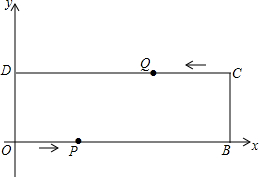 已知长方形的生活小区OBCD的边长分别为40米和130米,如图,建立平面直角坐标系,“创文明城市”宣传车点P从点O出发,沿OB运动至点B停止,宣传车点Q从点C出发,沿CD运动至点D停止,两车同时出发,速度都是1米/秒;宣传车音响半径可达25米,(两点间距离公式:|AB|=$\sqrt{({x}_{A}-{x}_{B})^{2}+({y}_{A}-{y}_{B})^{2}}$)
已知长方形的生活小区OBCD的边长分别为40米和130米,如图,建立平面直角坐标系,“创文明城市”宣传车点P从点O出发,沿OB运动至点B停止,宣传车点Q从点C出发,沿CD运动至点D停止,两车同时出发,速度都是1米/秒;宣传车音响半径可达25米,(两点间距离公式:|AB|=$\sqrt{({x}_{A}-{x}_{B})^{2}+({y}_{A}-{y}_{B})^{2}}$)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 18 | B. | 21 | C. | 24 | D. | 19.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com