
如图,把一个等腰直角三角形放在间距是1的横格纸上,三个顶点都在横格上,则此三角形的斜边长是( )
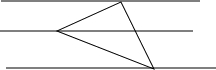
A.3 B. C.2
C.2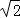 D.2
D.2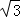
B【考点】全等三角形的判定与性质;勾股定理;等腰直角三角形.
【分析】作BD⊥a于D,CE⊥a于E则∠BDA=∠AEC=90°,证出∠ABD=∠CAE,由AAS证明△ABD≌△CAE,得出对应边相等AE=BD=1,由勾股定理求出AC,再由勾股定理求出BC即可.
【解答】解:如图所示:作BD⊥a于D,CE⊥a于E,
则∠BDA=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠CAE+∠BAD=90°,
∴∠ABD=∠CAE,
在△ABD和△CAE中,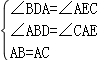 ,
,
∴△ABD≌△CAE(AAS),
∴AE=BD=1,
∵CE=2,
∴由勾股定理得:AB=AC=,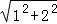 =
=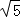 ,
,
∴BC=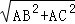 =
=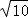 .
.
故选:B.
【点评】本题考查了全等三角形的判定与性质、等腰直角三角形的性质、勾股定理;熟练掌握勾股定理,通过作辅助线证明三角形全等是解决问题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
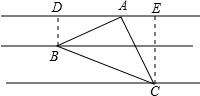
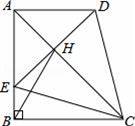
在四边形ABCD中,AD∥BC,∠ABC=90°,AB=BC,E为AB边上一点,∠BCE=15°,且AE=AD.连接DE交对角线AC于H,连接BH.下列结论正确的是 .(填序号)
①AC⊥DE;②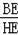
 =
=
 ;③CD=2DH;④
;③CD=2DH;④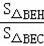
 =
=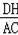
 .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
如图,我们把一个半圆与抛物线的一部分围成的封闭图形称为“果圆”.如果一条直线与果圆只有一个交点,则这条直线叫做果圆的切线.已知A、B、C、D四点为果圆与坐标轴的交点,E为半圆的圆心,抛物线的解析式为y=x2﹣2x﹣3,AC为半圆的直径.
(1)分别求出A、B、C、D四点的坐标;
(2)求经过点D的果圆的切线DF的解析式;
(3)若经过点B的果圆的切线与x轴交于点M,求△OBM的面积.


查看答案和解析>>
科目:初中数学 来源: 题型:
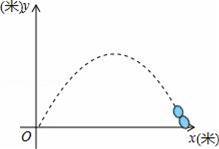
某广场有一喷水池,水从地面喷出,如图,以水平地面为x轴,出水点为原点,建立平面直角坐标系,水在空中划出的曲线是抛物线y=﹣x2+4x(单位:米)的一部分,则水喷出的最大高度是( )

A.4米 B.3米 C.2米 D.1米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com