
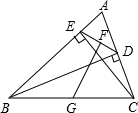
如图,在△ABC中,BD、CE是高,G、F分别是BC、DE的中点,连接GF,求证:GF⊥DE.
科目:初中数学 来源: 题型:
如图,已知△ABC,AC<AB.
(1)用直尺和圆规作出一条过点A的直线l,使得点C关于直线l的对称点落在边AB上(不写作法,保留作图痕迹);
(2)设直线l与边BC的交点为D,且∠C=2∠B,请你通过观察或测量,猜想线段AB、AC、CD之间的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠B=30°,∠C=45°,AC=2,点P是△ABC三条边上的任意一点.若△ACP为等腰三角形,在图中作出所有符合条件的点P,要求:
①尺规作图,不写作法,保留痕迹;
②若符合条件的点P不只一个,请标注P1、P2…
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠B、∠C的平分线BE,CD相交于点F,∠ABC=42°,∠A=60°,则∠BFC=( )

A.118° B.119° C.120° D.121°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com