

分析 (1)如图1,易求得∠BAD=∠DAC=∠EDC=40°,再结合∠B=∠C=∠ADE=50°,即可得到△ADE∽△ABD∽△ACD∽△DCE;
(2)如图2,根据∠EDF=∠B及三角形外角性质可得∠BFD=∠CDE,再根据∠B=∠C即可得到△BFD∽△CDE;
(3)①如图2,由(2)得△BFD∽△CDE,则有$\frac{BF}{CD}$=$\frac{DF}{ED}$,由D是BC的中点可得$\frac{BF}{BD}$=$\frac{DF}{ED}$.再根据∠B=∠EDF即可得到△BDF∽△DEF;
②由∠B=∠C=50°可得∠BAC=80°,AB=AC,再由BD=CD可得AD⊥BC.若△DEF与△ABC相似,由△BDF∽△DEF可得△BDF与△ABC相似,从而得到∠BDF=∠BAC=80°,或∠BDF=∠C=50°,即可解决问题.
解答 (1)解:如图1,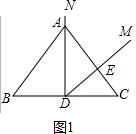
与△ADE相似的有△ABD、△ACD、△DCE.
提示:易求得∠BAD=∠DAC=∠EDC=40°,
又∵∠B=∠C=∠ADE=50°,
∴△ADE∽△ABD∽△ACD∽△DCE;
(2)证明:如图2,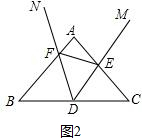
∵∠FDC是△BFD的一个外角,
∴∠FDC=∠B+∠BFD.
∵∠FDC=∠FDE+∠EDC,∠EDF=∠B=50°,
∴∠BFD=∠CDE.
∵∠B=∠C=50°,
∴△BFD∽△CDE;
(3)①证明:如图2,
由(2)得△BFD∽△CDE,
∴$\frac{BF}{CD}$=$\frac{DF}{ED}$.
∵D是BC的中点,
∴BD=CD,
∴$\frac{BF}{BD}$=$\frac{DF}{ED}$.
又∵∠B=∠EDF=50°,
∴△BDF∽△DEF.
②10°或40°.
提示:解:连接AD,如图3,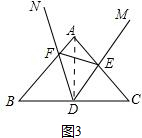
∵∠B=∠C=50°,
∴∠BAC=80°,AB=AC.
∵BD=CD,
∴AD⊥BC.
若△DEF与△ABC相似,
∵△BDF∽△DEF,
∴△BDF与△ABC相似,
∴∠BDF=∠BAC=80°,或∠BDF=∠C=50°,
∴∠ADF=90°-80°=10°,或∠ADF=90°-50°=40°,
∴当(2)中的旋转角为10°或40°时,△DEF与△ABC相似.
点评 本题主要考查了相似三角形的判定与性质、等腰三角形的判定与性质、三角形的外角性质、三角形内角和定理等知识,并考查了K型相似(若∠B=∠C=∠EDF,则△BDF∽△CED)及其推论(若△BDF∽△CED,BD=CD,则△BDF∽△CED∽△DEF),应熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.
如图,已知直线的函数表达式为y=-$\frac{4}{3}$x+8,且l与x轴,y轴分别交于A,B两点,动点Q从B点开始在线段BA上以每秒2个单位的速度向点A移动,同时动点P从A点开始在线段AO上以每秒1个单位的速度向O点移动,设点Q、P移动时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
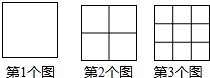 观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…
观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (3,4) | B. | (3,-4) | C. | (-4,3) | D. | (4,-3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com