Question

16．类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整．
原题：如图1，在?ABCD中，点E是BC边上的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若$\frac{AF}{EF}$=3，求$\frac{CD}{CG}$的值．
（1）尝试探究
在图1中，过点E作EH∥AB交BG于点H，则AB和EH的数量关系是AB=3EH，CG和EH的数量关系是CG=2EH，$\frac{CD}{CG}$的值是$\frac{3}{2}$
（2）类比延伸
如图2，在原题的条件下，若$\frac{AF}{EF}$=m（m≠0），则$\frac{CD}{CG}$的值是$\frac{m}{2}$（用含m的代数式表示），试写出解答过程．
（3）拓展迁移
如图3，梯形ABCD中，DC∥AB，点E是BC延长线上一点，AE和BD相交于点F，若$\frac{AB}{CD}$=a，$\frac{BC}{BE}$=b（a＞0，b＞0），则$\frac{AF}{EF}$的值是ab（用含a，b的代数式表示）．

Answer 1

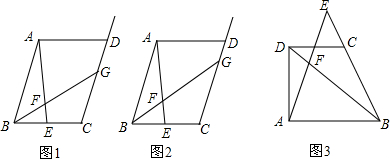
分析 （1）本问体现“特殊”的情形，$\frac{AF}{EF}$=3是一个确定的数值．如答图1，过E点作平行线，构造相似三角形，利用相似三角形和中位线的性质，分别将各相关线段均统一用EH来表示，最后求得比值；
（2）本问体现“一般”的情形，$\frac{AF}{EF}$=m不再是一个确定的数值，但（1）问中的解题方法依然适用，如答图2所示．
（3）本问体现“类比”与“转化”的情形，将（1）（2）问中的解题方法推广转化到梯形中，如答图3所示

解答 解：（1）依题意，过点E作EH∥AB交BG于点H，如图1所示．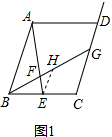

则有△ABF∽△EHF，
∴$\frac{AB}{EH}$=$\frac{AF}{EF}$=3，
∴AB=3EH．
∵?ABCD，EH∥AB，
∴EH∥CD，
又∵E为BC中点，
∴EH为△BCG的中位线，
∴CG=2EH．
∴$\frac{CD}{CG}=\frac{AB}{CG}=\frac{3EH}{2EH}=\frac{3}{2}$．
故答案为：AB=3EH；CG=2EH；$\frac{3}{2}$．
（2）如图2所示，作EH∥AB交BG于点H，则△EFH∽△AFB．

∴$\frac{AB}{EH}=\frac{AF}{EF}=m$．
∴AB=mEH．
∵AB=CD，
∴CD=mEH．
∵EH∥AB∥CD，
∴△BEH∽△BCG．
∴$\frac{CG}{EH}=\frac{BC}{BE}$=2，
∴CG=2EH．
∴$\frac{CD}{CG}=\frac{mEH}{2EH}$=$\frac{m}{2}$．
故答案为：$\frac{m}{2}$．
（3）如图3所示，过点E作EH∥AB交BD的延长线于点H，则有EH∥AB∥CD．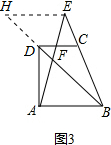

∵EH∥CD，
∴△BCD∽△BEH，
∴$\frac{CD}{EH}=\frac{BC}{BE}$=b，
∴CD=bEH．
又$\frac{AB}{CD}=a$，
∴AB=aCD=abEH．
∵EH∥AB，
∴△ABF∽△EHF，
∴$\frac{AF}{EF}=\frac{AB}{EH}=\frac{abEH}{EH}$=ab．
故答案为：ab．

点评 本题的设计独具匠心：由平行四边形中的一个特殊的例子出发（第1问），推广到平行四边形中的一般情形（第2问），最后再通过类比、转化到梯形中去（第3问）．各种图形虽然形式不一，但运用的解题思想与解题方法却是一以贯之：即通过构造相似三角形，得到线段之间的比例关系，这个比例关系均统一用同一条线段来表达，这样就可以方便地求出线段的比值．本题体现了初中数学的类比、转化、从特殊到一般等思想方法，有利于学生触类旁通、举一反三．