
分析 (1)根据方程x2-2(k-3)x+k2-4k-1=0有实数根,即△≥0,求出k的取值范围即可;
(2)把x=1代入方程,得到k的一元二次方程,求出k的值即可;
(3)根据根与系数的关系得到x1+x2=2k-6,x1•x2=k2-4k-1,结合题意列出k的方程,求出k的值;
(4)设方程的两个根分别为x,$\frac{m}{x}$,根据题意得到m=k2-4k+4-4-1=(k-2)2-5,根据二次函数的性质求出m的最小值.
解答 解:(1)∵关于x的方程x2-2(k-3)x+k2-4k-1=0有实数根,
∴△≥0,
∴△=4(k-3)2-4(+k2-4k-1)≥0,即-2k+10≥0,
∴k≤5;
(2)∵方程x2-2(k-3)x+k2-4k-1=0有一根为1,
∴把x=1代入方程得:1-2(k-3)+k2-4k-1=0,
整理得:k2-6k+6=0,
解得k1=3+$\sqrt{3}$,k2=3-$\sqrt{3}$;
(3)∵存在实数k,使方程x2-2(k-3)x+k2-4k-1=0的两个实数根的倒数和等0,则令方程的两个根分别为x1,x2,
∴x1+x2=2k-6,x1•x2=k2-4k-1,
又∵$\frac{1}{{x}_{1}}$+$\frac{1}{{x}_{2}}$=0,即$\frac{{x}_{1+{x}_{2}}}{{x}_{1•{x}_{2}}}$=0,
∴$\frac{2k-6}{{k}^{2}-4k-1}$=0,即2k-6=0,
∴k=3;
(4)∵以方程x2-2(k-3)x+k2-4k-1=0的两个根为横坐标、纵坐标的点恰在反比例函数$y=\frac{m}{x}$的图象上,
∴设方程的两个根分别为x,$\frac{m}{x}$,
∴x•$\frac{m}{x}$=k2-4k-1,即m=k2-4k-1,
∴m=k2-4k+4-4-1=(k-2)2-5,即m=(k-2)2-5,
∴当k=2时m有最小值为-5,
∴m的最小值为-5.
点评 本题考查了一元二次方程ax2+bx+c=0(a≠0)的根的判别式△=b2-4ac:当△>0,方程有两个不相等的实数根;当△=0,方程有两个相等的实数根;当△<0,方程没有实数根.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
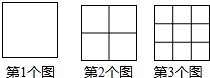 观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…
观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…查看答案和解析>>
科目:初中数学 来源: 题型:选择题
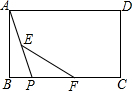 如图,矩形ABCD中,点P从点B出发沿BC向点C运动,E、F分别是AP、PC的中点,则EF的长度( )
如图,矩形ABCD中,点P从点B出发沿BC向点C运动,E、F分别是AP、PC的中点,则EF的长度( )| A. | 逐渐增大 | B. | 逐渐减小 | C. | 不变 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3℃ | B. | 8℃ | C. | 11℃ | D. | 17℃ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com