
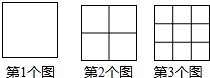
 观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…
观察下面图形我们可以发现:第1个图中有1个正方形,第2个图中有5个正方形,按照这种规律变化下去…分析 (1)由图可知结果;
(2)根据第1个图,第2个图,第3个图,可得变化规律;
(3)根据题意分析可得出规律:即是后一个图在前一个图的基础上添加这个图的序号的平方即可得出;
(4)看2015是否为一个正整数平方的形式.
解答 解:(1)由图知:第3个图中有9+4+1=14个正方形,
故答案为:14;
(2)∵第1个图中有1个正方形;
第2个图中共有5=2×2+1个正方形;
第3个图中共有14=3×3+5个正方形;
可以发现:第2个图形比第1个图形多:5-1=4=22个;
第3个图形比第2个图形多:14-5=9=32个,
∴第4个图形比第3个图形多42=16个.
故答案为:16;
(3)由(2)的规律可得:第n个图比前一个图形多n2个.
故答案为:n2;
(4)∵$\sqrt{2015}$不能开平方,
∴不存在某个图形,它比前一个图形增加2015个正方形.
点评 此题主要考查了图形的变化类,此题是一道找规律的题目,这类题型在中考中经常出现.对于找规律的题目首先应找出哪些部分发生了变化,是按照什么规律变化的.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
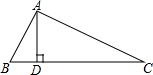 如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )
如图:在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,BD=1,AC=$2\sqrt{5}$,则AD等于( )| A. | 1 | B. | $\frac{{\sqrt{3}}}{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com