
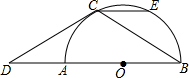
 如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.
如图,AB是半圆O的直径,点C在半圆上,过点C的切线交BA的延长线于点D,CD=CB,CE∥AB交半圆于点E.分析 (1)连接AC,根据切线的性质以及等腰三角形的性质得出∠D=∠ACD=∠ABC,根据圆周角定理得出∠ACB=90°,然后根据三角形内角和定理即可求得∠D的度数;
(2)连接OC、BE,先证得△AOC是等边三角形,然后证得四边形COBE是平行四边形即可证得结论.
解答  (1)解:连接AC,
(1)解:连接AC,
∵CD是⊙O的切线,
∴∠ACD=∠ABC,
∵AB是直径,
∴∠ACB=90°,
∵CD=CB,
∴∠D=∠ABC,
∴∠D=∠ACD=∠ABC,
∵∠D+∠ACD+∠ABC+∠ACB=90°,
∴∠D=30°;
(2)证明:连接OC、BE,
∵∠D=∠ACD=30°,
∴∠CAB=60°,
∵OA=OC,
∴△AOC是等边三角形,
∴AC=OC,∠AOC=60°,
∵CE∥AB,
∴AC=EB,
∴四边形ACEB是等腰梯形,OC=BE,
∴∠CAB=∠EBA=60°,
∴∠AOC=∠EBA=60°,
∴OC∥BE,
∴四边形COBE是平行四边形,
∵OC=OB,
∴以点C,O,B,E为顶点的四边形是菱形.
点评 本题考查了切线的性质,圆周角定理,等腰梯形的判定和性质,菱形的判定等,作出辅助线构建直角三角形和等边三角形是解题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
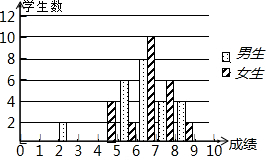 为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下
为了迎接体育中考,初三7班的体育老师对全班48名学生进行了一次体能模拟测试,得分均为整数,满分10分,成绩达到6分以上(包括6分)为合格,成绩达到9分以上(包括9分)为优秀,这次模拟测试中男、女生全部成绩分布的条形统计图如下| 平均分 | 方差 | 中位数 | 合格率 | 优秀率 | |
| 男生 | 6.9 | 2.4 | 7 | 91.7% | 16.7% |
| 女生 | 7 | 1.3 | 7 | 83.3% | 8.3% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com