计算:①832+83×34+172=10000,②103×97=9997．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

7．计算：
①83²+83×34+17²=10000；
②103×97=9997．

分析 ①利用完全平方公式计算可得；
②利用平方差公式计算可得．

解答解：①原式=83²+2×83×17+17²=（83+17）2=100²=10000；
②103×97=（100+3）×（100-3）=100²-3²=10000-9=9997；
故答案为：10000，9997．

点评本题主要考查有理数的混合运算，利用完全平方公式和平方差公式简便计算是解题的关键．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

13．

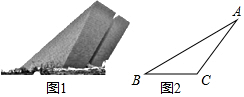位于合肥滨湖新区的渡江战役纪念馆，实物图如图1所示，示意图如图2所示．某学校数学兴趣小组通过测量得知，纪念馆外轮廓斜坡AB的坡度i=1：$\sqrt{3}$，底基BC=50m，∠ACB=135°，求馆顶A离地面BC的距离．（结果精确到0.1m，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

14．

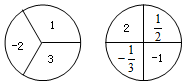如图，甲转盘被分成 3 个面积相等的扇形，乙转盘被分成 4 个面积相等的扇形，每一个扇形都标有相应的数字．同时转动两个转盘，当转盘停止后，设甲转盘中指针所指区域内的数字为x，乙转盘中指针所指区域内的数字为y（当指针指在边界线上时，重转，直到指针指向一个区域为止）．
（1）请你用画树状图或列表格的方法，求点（x，y）落在第二象限内的概率；
（2）直接写出点（x，y）落在函数y=-$\frac{1}{x}$图象上的概率．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

15．已知扇形的圆心角为60°，半径长为12，则该扇形的弧长为4π．（结果保留π）

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

2．

如图，把△EFP按图示方式放置在菱形ABCD中，使得顶点E、F、P分别在线段AB、AD、AC上，已知EP=FP=4，EF=$4\sqrt{3}$，∠BAD=60°，且AB＞$4\sqrt{3}$．给出下列结论：
①∠EPF=120°；
②若AP=6，则AE+AF=$8\sqrt{3}$
③若△EFP的三个顶点E，F，P分别在线的AB，AD，AC上运动，则AP的长存在最大值8；
④若△EFP的三个顶点E，F，P分别在线的AB，AD，AC上运动，则AP的长存在最小值4．
以上结论正确的是①③④．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

12．根据图形填空：