
 ��ͼ���ѡ�EFP��ͼʾ��ʽ����������ABCD�У�ʹ�ö���E��F��P�ֱ����߶�AB��AD��AC�ϣ���֪EP=FP=4��EF=$4\sqrt{3}$����BAD=60�㣬��AB��$4\sqrt{3}$���������н��ۣ�
��ͼ���ѡ�EFP��ͼʾ��ʽ����������ABCD�У�ʹ�ö���E��F��P�ֱ����߶�AB��AD��AC�ϣ���֪EP=FP=4��EF=$4\sqrt{3}$����BAD=60�㣬��AB��$4\sqrt{3}$���������н��ۣ����� ����P��PG��EF��G����ֱ�������μ��ɵõ����ۢ���ȷ����ͼ2������P��PM��AB��M��PN��AD��N��֤����ABC�ա�ADC��Rt��PME��Rt��PNF���������AE+AF=8$\sqrt{3}$�ó����ۢڴ�����ͼ3����EF��AC����P��EF���Ҳ�ʱ��AP�����ֵ�������жϳ�����ȷ����EF��AC����P��EF�����ʱ��AP����Сֵ��ֱ�������μ����жϳ�����ȷ��
��� 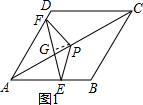 �⣺��ͼ1������P��PG��EF��G��
�⣺��ͼ1������P��PG��EF��G��
��PE=PF��
��FG=EG=$\frac{1}{2}$EF=2$\sqrt{3}$����FPG=��EPG=$\frac{1}{2}$��EPF��
��Rt��FPG��sin��FPG=$\frac{FG}{PF}$=$\frac{2\sqrt{3}}{4}$=$\frac{\sqrt{3}}{2}$��
���FPG=60�㣬
���EPF=2��FPG=120�㣻�ʢ���ȷ��
��ͼ2������P��PM��AB��M��PN��AD��N��
���ı���ABCD�����Σ�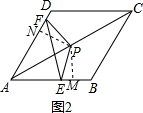
��AD=AB��DC=BC��
���DAC=��BAC��
��PM=PN��
��Rt��PME��Rt��PNF��$\left\{\begin{array}{l}{PM=PN}\\{PE=PF}\end{array}\right.$��
��Rt��PME��Rt��PNF��
��FN=EM��
��Rt��PMA�У���PMA=90�㣬��PAM=$\frac{1}{2}$��DAB=30�㣬
��AM=AP•cos30��=6��$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$��
ͬ��AN=3$\sqrt{3}$��
��AE+AF=��AM-EM��+��AN+NF��=6$\sqrt{3}$���ʢڴ���
��ͼ3������P��EF�ұ�ʱ��
�ߡ�BAD=60�㣬��EPF=120�㣬
���BAD+��EPF=180�㣬
���A��E��P��F�ĵ㹲Բ��
��AP�Ǵ�Բ��ֱ��ʱ��AP���
��PE=PF��
��EF��ACʱ��AP���
��AC��EF���ڵ�O��
��PE=PF��
��OF=$\frac{1}{2}$EF=2$\sqrt{3}$��
�ߡ�FPA=60�㣬
��OP=2��
�ߡ�BAD=60�㣬
���FAO=30�㣬
��AO=6��
��AP=AO+PO=8���ʢ���ȷ��
����P��EF�����ʱ������P'��
��EF�Ҳ�ȡһ��Pʹ��EPF=��EP'F=120�㣬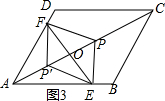
ͬ��EF��ACʱ��AP���AP'��С��
ͬ��AP��=AO-OP=4��
����Сֵ��4���ʢ���ȷ��
�ʴ�Ϊ�٢ۢܣ�
���� �������ı����ۺ��⣬��Ҫ���������ε����ʣ���ֱ�������Σ�ȫ�������ε��ж������ʣ���ֵ���⣬���������ε����ʣ���ٵĹؼ����������߹���ֱ�������Σ���ڵĹؼ��ǹ����ֱ�������Σ��жϳ�Rt��PME��Rt��PNF����ۢܵĹؼ����жϳ���A��E��P��F�ĵ㹲Բ�ó�AP����AP'��С��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | -6 | C�� | -2��6 | D�� | -2��30 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
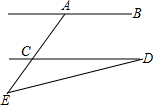 ��ͼ��ʾ��AB��CD����CAB=116�㣬��E=40�㣬���D�Ķ����ǣ�������
��ͼ��ʾ��AB��CD����CAB=116�㣬��E=40�㣬���D�Ķ����ǣ�������| A�� | 24�� | B�� | 26�� | C�� | 34�� | D�� | 22�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 5��1010ǧ�� | B�� | 50��109ǧ�� | C�� | 5��109ǧ�� | D�� | 0.5��1011ǧ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com