练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    8．已知x2-2x-3=0，则2x2-4x的值为（　　）
    A．6B．-6C．-2或6D．-2或30

    分析 原式提取2变形后，将已知等式变形后代入计算即可求出值．

    解答 解：∵x2-2x-3=0，即x2-2x=3，
    ∴原式=2（x2-2x）=6，
    故选A

    点评 此题考查了代数式求值，利用了整体代入的思想，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    18．函数y=$\frac{\sqrt{x+1}}{x-2}$中，自变量x的取值范围是x≥-1且x≠2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

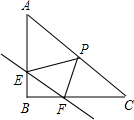    19．如图，在Rt△ABC中，∠B=90°，直线EF分别交两直角边AB、BC与E、F两点，且EF∥AC，P是斜边AC的中点，连接PE，PF，且AB=$\frac{6}{5}$，BC=$\frac{8}{5}$．
    （1）当E、F均为两直角边的中点时，求证：四边形EPFB是矩形，并求出此时EF的长；
    （2）设EF的长度为x（x＞0），当∠EPF=∠A时，用含x的代数式表示EP的长；
    （3）设△PEF的面积为S，则当EF为多少时，S有最大值，并求出该最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．观察下列等式14×451=154×41；
    15×561=165×51；21×132=231×12；
    25×572=275×52；32×253=352×23…
    以上每个等式中两边数字是分别对称的，且每个等式中组成两位数与三位数的数字之间是具有相同的规律，我们称这类等式为“数字对称等式”，设这类等式左边两位数的十位数字为a，个位数字为b，且2≤a+b≤9，写出表示“数字对称等式”一般规律的式子（含a，b）是（10a+b）（110b+11a）=（110a+11b）（10b+a）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    3．抛物线y=-（a-8）2+2的顶点坐标是（　　）
    A．（ 2，8 ）B．（ 8，2 ）C．（-8，2 ）D．（-8，-2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

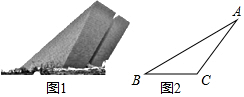    13．位于合肥滨湖新区的渡江战役纪念馆，实物图如图1所示，示意图如图2所示．某学校数学兴趣小组通过测量得知，纪念馆外轮廓斜坡AB的坡度i=1：$\sqrt{3}$，底基BC=50m，∠ACB=135°，求馆顶A离地面BC的距离．（结果精确到0.1m，参考数据：$\sqrt{2}$≈1.41，$\sqrt{3}$≈1.73）

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．已知一次函数y1=kx+b（k＜0）与反比例函数y2=$\frac{m}{x}$（m≠0）的图象相交于A、B两点，其横坐标分别是-1和3，当y1＞y2，实数x的取值范围是（　　）
    A．x＜-1或0＜x＜3B．-1＜x＜0或0＜x＜3C．-1＜x＜0或x＞3D．0＜x＜3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图，AB、BC是⊙O的弦，OM∥BC交AB于M，若∠AOC=100°，则∠AMO=50°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，把△EFP按图示方式放置在菱形ABCD中，使得顶点E、F、P分别在线段AB、AD、AC上，已知EP=FP=4，EF=$4\sqrt{3}$，∠BAD=60°，且AB＞$4\sqrt{3}$．给出下列结论：
    ①∠EPF=120°；
    ②若AP=6，则AE+AF=$8\sqrt{3}$
    ③若△EFP的三个顶点E，F，P分别在线的AB，AD，AC上运动，则AP的长存在最大值8；
    ④若△EFP的三个顶点E，F，P分别在线的AB，AD，AC上运动，则AP的长存在最小值4．
    以上结论正确的是①③④．

    查看答案和解析>>

    同步练习册答案