练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
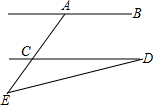
    9．如图所示，AB∥CD，∠CAB=116°，∠E=40°，则∠D的度数是（　　）
    A．24°B．26°C．34°D．22°

    分析 先根据平行线的性质得到∠ACD=180°-∠CAB=64°，然后根据三角形外角性质得∠D=∠ACD-∠E=24°．

    解答 解：∵AB∥CD，∠CAB=116°，
    ∴∠ACD=180°-∠CAB=64°，
    ∵∠E=40°，
    ∴∠D=∠ACD-∠E=24°．
    故选：A．

    点评 本题考查了平行线性质，关键是熟悉两直线平行，同位角相等；两直线平行，同旁内角互补；两直线平行，内错角相等，同时考查了三角形外角性质．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

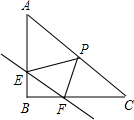    19．如图，在Rt△ABC中，∠B=90°，直线EF分别交两直角边AB、BC与E、F两点，且EF∥AC，P是斜边AC的中点，连接PE，PF，且AB=$\frac{6}{5}$，BC=$\frac{8}{5}$．
    （1）当E、F均为两直角边的中点时，求证：四边形EPFB是矩形，并求出此时EF的长；
    （2）设EF的长度为x（x＞0），当∠EPF=∠A时，用含x的代数式表示EP的长；
    （3）设△PEF的面积为S，则当EF为多少时，S有最大值，并求出该最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．已知一次函数y1=kx+b（k＜0）与反比例函数y2=$\frac{m}{x}$（m≠0）的图象相交于A、B两点，其横坐标分别是-1和3，当y1＞y2，实数x的取值范围是（　　）
    A．x＜-1或0＜x＜3B．-1＜x＜0或0＜x＜3C．-1＜x＜0或x＞3D．0＜x＜3

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    17．如图，AB、BC是⊙O的弦，OM∥BC交AB于M，若∠AOC=100°，则∠AMO=50°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

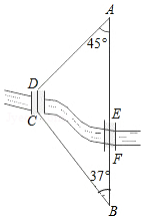    4．如图，A，B两地之间有条河，原来从A地到B地需要经过桥DC，沿折线A→D→C→B到达，现在新建了桥EF，可直接沿直线AB从A地到达B地．已知BC=11km，∠A=45°，∠B=37°，桥DC和AB平行，桥DC与桥EF的长相等．
    （1）求点D到直线AB的距离；
    （2）现在从A地到B地可比原来少走多少路程？
    （结果保留小数点后一位．参考数据：$\sqrt{2}$≈1.41，sin37°≈0.60，cos37°≈0.80）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

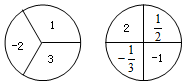    14．如图，甲转盘被分成 3 个面积相等的扇形，乙转盘被分成 4 个面积相等的扇形，每一个扇形都标有相应的数字．同时转动两个转盘，当转盘停止后，设甲转盘中指针所指区域内的数字为x，乙转盘中指针所指区域内的数字为y（当指针指在边界线上时，重转，直到指针指向一个区域为止）．
    （1）请你用画树状图或列表格的方法，求点（x，y）落在第二象限内的概率；
    （2）直接写出点（x，y）落在函数y=-$\frac{1}{x}$图象上的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

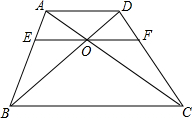    5．如图，四边形ABCD，AD∥BC，AD=m，BC=n，EF∥AD，经过点O，求EF的长为（　　）
    A．$\frac{m+n}{mn}$B．$\frac{2mn}{m+n}$C．$\frac{mn}{m+n}$D．$\frac{m+n}{2mn}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    2．如图，把△EFP按图示方式放置在菱形ABCD中，使得顶点E、F、P分别在线段AB、AD、AC上，已知EP=FP=4，EF=$4\sqrt{3}$，∠BAD=60°，且AB＞$4\sqrt{3}$．给出下列结论：
    ①∠EPF=120°；
    ②若AP=6，则AE+AF=$8\sqrt{3}$
    ③若△EFP的三个顶点E，F，P分别在线的AB，AD，AC上运动，则AP的长存在最大值8；
    ④若△EFP的三个顶点E，F，P分别在线的AB，AD，AC上运动，则AP的长存在最小值4．
    以上结论正确的是①③④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解方程 2x+1=-3（x-5）

    查看答案和解析>>

    同步练习册答案