
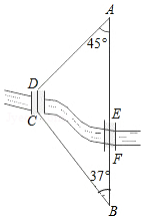
 如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.
如图,A,B两地之间有条河,原来从A地到B地需要经过桥DC,沿折线A→D→C→B到达,现在新建了桥EF,可直接沿直线AB从A地到达B地.已知BC=11km,∠A=45°,∠B=37°,桥DC和AB平行,桥DC与桥EF的长相等.分析 (1)过点D作DH⊥AB于H,DG∥CB交AB于G,根据平行四边形的判定得出DCBG为平行四边形,在Rt△DGH中,根据DH=DG•sin37,即可求出点D到直线AB的距离;
(2)根据(1)先求出GH、AD和AH的长,再根据两条路线路程之差为AD+DG-AG,代值计算即可得出答案.
解答 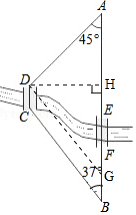 解:(1)如图,过点D作DH⊥AB于H,DG∥CB交AB于G,
解:(1)如图,过点D作DH⊥AB于H,DG∥CB交AB于G,
∵DC∥AB,
∴四边形DCBG为平行四边形.
∴DC=GB,GD=BC=11.
在Rt△DGH中,
DH=DG•sin37°≈11×0.60=6.60,
∴点D到直线AB的距离是6.60km;
(2)根据(1)得:
GH=DG•cos37°≈11×0.80≈8.80,
在Rt△ADH中,
AD=$\sqrt{2}$DH≈1.41×6.60≈9.31.
AH=DH≈6.60,
∵两条路线路程之差为AD+DG-AG,
∴AD+DG-AG=(9.31+11)-(6.60+8.80)≈4.9(km).
即现在从A地到B地可比原来少走约4.9km.
点评 此题考查了解直角三角形的应用,将梯形中的问题转化为三角形问题是解决梯形问题的常用方法,常作的辅助线有平移腰、平移对角线、作高等.


 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 各有一个角是30°的两个等腰三角形 | |
| B. | 有两边之比都等于2:3的两个三角形 | |
| C. | 各有一个角是120°的两个等腰三角形 | |
| D. | 各有一个角是直角的两个三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系内,作出下列函数的图象.
在平面直角坐标系内,作出下列函数的图象.| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | 4.5 | 3.5 | 2.5 | 1.5 | 0.5 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com