Question

16．阅读材料：
（1）如图1，△ABC中，AD是∠BAC的平分线，且BD=CD，求证：AB=AC．
小明解决上面的问题的思路是，延长AD到点E，使DE=AD，连接BE，从完成此题，请按照小明的思路将此题补充完整．
（2）等腰△ABC△DCE中，∠BAC+∠CDE=180°，AB=AC，DC=DE，连接BE，取BE的中点P，连接PA，PD．
①如图2，当∠BAC=∠CDE=90°，猜想并验证PA与PD的数量关系和位置关系．
②如图3，当∠BAC≠∠CDE≠90°时，猜想并验证PA与PD的位置关系．

Answer 1

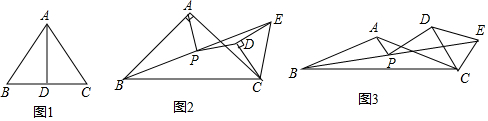
分析 （1）延长AD到点E，使DE=AD，连接BE，由SAS证明△BDE≌△CDA，得出BE=AC，∠E=∠CAD，由角平分线得出∠BAD=∠CAD，∠E=∠BAD，证出AB=BE，即可得出结论；
（2）作辅助线，构建全等三角形，证明四边形PHCI是平行四边形，得PH=CI，PI=CH，∠PHC=∠PIC，再证明△AHP≌△PID，根据全等三角形的性质和四边形的内角和360°，得∠APD=90°，所以AP=PD且PA⊥PD；
（3）作辅助线，构建中点和平行四边形，先根据等腰三角形三线合一得：∠HAC=$\frac{1}{2}$∠BAC，∠CDI=$\frac{1}{2}$∠CDE，则∠HAC+∠CDI=90°，根据同角的余角相等得∠CDI=∠HCA，证明△AHC∽△CID，则$\frac{AH}{CI}=\frac{CH}{DI}$，$\frac{AH}{PH}$=$\frac{PI}{DI}$，从而得△AHP∽△PID，则∠HAP=∠DPI，利用周角的性质得：∠APD=90°，则AP⊥PD．

解答 （1）证明：延长AD到点E，使DE=AD，连接BE，如图1所示：
在△BDE和△CDA中，$\left\{\begin{array}{l}{DE=DA}&{\;}\\{∠BDE=∠CDA}&{\;}\\{BD=CD}&{\;}\end{array}\right.$，
∴△BDE≌△CDA（SAS），
∴BE=AC，∠E=∠CAD，
∵AD平分∠BAC，
∴∠BAD=∠CAD，
∴∠E=∠BAD，
∴AB=BE，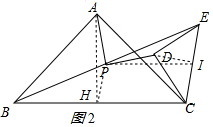
∴AB=AC；
（2）解：①PA=PD且PA⊥PD，理由如下：
取BC的中点H，CE的中点I，连接AH、PH、PI、DI，如图2所示：
∵∠BAC=∠CDE=90°，AB=AC，DC=DE，
∴△ABC和△CDE是等腰直角三角形，
∴AH⊥BC，DI⊥CE，
∴∠AHC=∠DIC=90°，
∵P、H、I分别是BE、BC、EC的中点，
∴PH、PI是△BEC的中位线，AH=$\frac{1}{2}$BC=CH，DI=$\frac{1}{2}$BC=CI
∴PH∥EC，PI∥BC，
∴四边形PHCI是平行四边形，
∴PH=CI，PI=CH，∠PHC=∠PIC∴AH=PI，∠AHP=∠PID，PH=DI，
∴△AHP≌△PID，
∴AP=PD，∠HAP=∠DPI，
∵∠HAP+∠APH+∠AHP+∠AHB=180°+90°=270°，
∴∠HAP+∠APH+∠PHB=270°，
∴∠DPI+APH+∠IPH=270°，
∴∠APD=360°-270°=90°，
∴PA⊥PD；
（3）解：如图3，AP⊥PD，理由如下：
取BC的中点H，EC的中点I，连接AH、PH、PI、DI，
同理可得：四边形PHCI是平行四边形，
∴PI=CH，PH=CI，
∵AB=AC，H是BC的中点，
∴AH平分∠BAC，AH⊥BC，
∴∠HAC=$\frac{1}{2}$∠BAC，∠AHC=90°，
同理，∠CDI=$\frac{1}{2}$∠CDE，∠DIC=90°，
∵∠BAC+∠CDE=180°，
∴∠HAC+∠CDI=90°，
∵∠HAC+∠HCA=90°，
∴∠CDI=∠HCA，
∵∠AHC=∠DIC=90°，
∴△AHC∽△CID，
∴$\frac{AH}{CI}=\frac{CH}{DI}$，
∴$\frac{AH}{PH}$=$\frac{PI}{DI}$∵∠AHC=∠DHI，∠PHC=∠PIC，
∴∠AHC-∠PHC=∠DIC-∠PIC，即∠AHP=∠DIP，
∴△AHP∽△PID，
∴∠HAP=∠DPI，
∵∠APH+∠HAP+∠AHP+∠AHB=180°+90°=270°，
∴∠HAP+∠APH+∠PHB=270°，
∵PI∥BC，
∴∠PHB=∠HPI，
∴∠DPI+∠APH+∠HPI=270°，
∵∠DPI+∠APH+∠HPI+∠APD=360°，
∴∠APD=90°，
∴AP⊥PD．

点评 本题是三角形综合题目，考查了全等三角形的判定与性质、相似三角形的性质和判定、平行四边形的判定与性质及等腰三角形的性质，图形比较复杂，有一定难度，通过作辅助线，证明三角形全等和三角形相似是解决问题的关键．