
【题目】四边形ABCD是⊙O的内接四边形,连结AC、BD,且DA=DB.
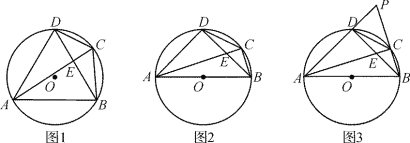
(1)如图1,∠ADB=60°.求证:AC=CD+CB.
(2)如图2,∠ADB=90°.
①求证:AC=![]() CD+CB.
CD+CB.
②如图3,延长AD、BC交于点P,且DC=![]() CB,探究线段BD与DP的数量关系,并说明理由.
CB,探究线段BD与DP的数量关系,并说明理由.
【答案】(1)见解析;(2)①AC =![]() CD +CB,理由见解析;②BD=2DP,理由见解析
CD +CB,理由见解析;②BD=2DP,理由见解析
【解析】
(1)在AC上截取AF=BC,连结DF,可证△DAF≌△DBC,然后证明△DFC是等边三角形,即可得到AC=CD+CB;
(2)在AC上截取AF=BC,连结DF,可证△DAF≌△DBC,然后得到△DFC是等腰直角三角形,得到FC =![]() DC,即可得到结论;
DC,即可得到结论;
(3)过点D作DF⊥AC于点F,可证△CFD是等腰直角三角形,结合DC=![]() CB,然后得到DF=CB,可证△DFE≌△CBE,得到DE=BE=
CB,然后得到DF=CB,可证△DFE≌△CBE,得到DE=BE=![]() BD,然后证明△ADE≌△BDP,即可得到结论成立.
BD,然后证明△ADE≌△BDP,即可得到结论成立.
解:(1)如图1,证明:在AC上截取AF=BC,连结DF.
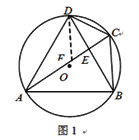
在△DAF与△DBC中,
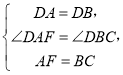
∴△DAF≌△DBC(SAS),
∴DF=DC,∠CDB=∠ADF,
∵∠CDF=∠CDB +∠EDF=∠ADF +∠EDF=∠ADB=60,
∴△DFC为正三角形,
∴DC=FC,
∴AC=AF +FC=BC +CD.
(2)①AC =![]() CD +CB.
CD +CB.
理由:如图2,在AC上截取AF=BC,连结DF.
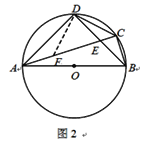
在△DAF与△DBC中,
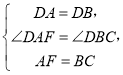
∴△DAF≌△DBC(SAS),
∴DF=DC,∠CDB=∠ADF,
∵∠CDF=∠CDB +∠EDF=∠ADF +∠EDF=∠ADB=90,
∴△DFC为等腰直角三角形,
∴FC =![]() DC,
DC,
∴AC=AF +FC=![]() CD +CB.
CD +CB.
②BD=2DP.
理由:如图3,过点D作DF⊥AC于点F,
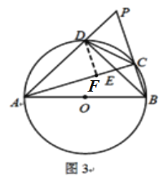
∵∠ACD=∠ABD=45°,
∴△CFD是等腰直角三角形,
∴CD=![]() DF,
DF,
∵CD=![]() CB,
CB,
∴DF=CB,
在△DFE和△CBE中,
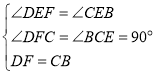 ,
,
∴△DFE≌△CBE(AAS),
∴DE=BE=![]() BD,
BD,
在△ADE和△BDP中,
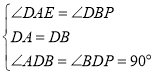 ,
,
∴△ADE≌△BDP(ASA),
∴DP=DE=BE=![]() BD,
BD,
∴BD=2DP.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() (k>0)的图像与矩形AOBC的边AC,BC分别交于点E、F,点C的坐标为(8,6),将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
(k>0)的图像与矩形AOBC的边AC,BC分别交于点E、F,点C的坐标为(8,6),将△CEF沿EF翻折,C点恰好落在OB上的点D处,则k的值为( )
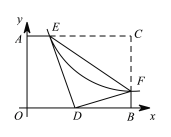
A.![]() B.6C.12D.
B.6C.12D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,直线y=-![]() x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
x+3与x轴相交于点A,与y轴相交于点B,点C(m,n)是第二象限内一点,以点C为圆心的圆与x轴相切于点E,与直线AB相切于点F.
(1)当四边形OBCE是矩形时,求点C的坐标;
(2)如图②,若⊙C与y轴相切于点D,求⊙C的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实施新课程改革后,学生的自主学习、合作交流能力有很大提高,张老师为了了解所教班级学生自主学习、合作交流的具体情况,对本班部分学生进行了为期半个月的跟踪调查,并将调查结果分成四类,A:特别好;B:好;C:一般;D:较差;并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题:
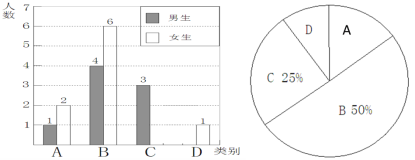
(1)本次调查中C类女生有 名,D类男生有 名;将上面的条形统计图补充完整;
(2)计算扇形统计图中D所占的圆心角是 ;
(3)为了共同进步,张老师想从被调查的A类和D类学生中分别选取一位同学进行“一帮一”互助学习,请用列表法或画树形图的方法求出所选两位同学恰好是一位男同学和一位女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.
(1)问:今年年初猪肉的价格为每千克多少元?
(2)某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,![]() 中,
中,![]() ,动点
,动点![]() 从
从![]() 出发,以每秒
出发,以每秒![]() 个单位长度的速度向终点
个单位长度的速度向终点![]() 运动,过点
运动,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 的平行线,与过点
的平行线,与过点![]() 且与
且与![]() 垂直的直线交于点
垂直的直线交于点![]() ,设点
,设点![]() 的运动时间为
的运动时间为![]() (秒)
(秒)![]()
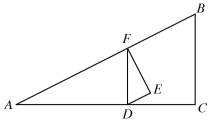
(1)用含![]() 的代数式表示线段
的代数式表示线段![]() 的长;
的长;
(2)求当点![]() 落在
落在![]() 边上时t的值;
边上时t的值;
(3)设![]() 与
与![]() 重合部分图形的面积为
重合部分图形的面积为![]() (平方单位),求
(平方单位),求![]() 与的
与的![]() 函数关系式;
函数关系式;
(4)连结![]() ,若将
,若将![]() 沿它自身的某边翻折,翻折前后的两个三角形形成菱形,直接写出此时
沿它自身的某边翻折,翻折前后的两个三角形形成菱形,直接写出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“泥兴陶,,是钦州的一张文化名片。钦州市某妮兴陶公司以每只60元的价格销售一种成本价为40元的文化纪念杯,每星期可售出100只。后来经过市场调查发现,每只杯子的售价每降低1元,则平均何星期可多买出10只。若该公司销售这种文化纪念杯要想平均每星期获利2240元,请回答:
(1)每只杯应降价多少元?
(2)在平均每星期获利不变的情况下,为尽可能让利于顾客,赢得市场,该公司应该按原售价的几折出售?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com