
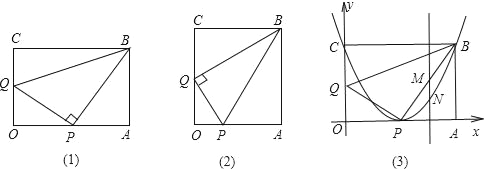
【题目】如图,已知矩形OABC,点P在边OA上(不与端点重合),点Q在边CO上(不与端点重合).
(1)如图(1),若∠BPQ=90°,且△OPQ与△PAB和△QPB相似,请写出表示这三个三角形相似的式子,并探究此时线段OQ、QB、BA之间的数量关系.
(2)若∠PQB=90°,且△OPQ与△PAB、△QPB都相似,如图(2),请重新写出表示这三个三角形相似的式子,并证明AB:OA=2![]() :3.
:3.
(3)在(1)中,若OA=8![]() ,OC=8,OP=
,OC=8,OP=![]() CQ.以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴,建立平面直角坐标系,如图(3),若某抛物线顶点为P,点B在抛物线上.
CQ.以矩形OABC的两边OA、OC所在的直线分别为x轴和y轴,建立平面直角坐标系,如图(3),若某抛物线顶点为P,点B在抛物线上.
①求此抛物线的解析式.
②过线段BP上一动点M(点M与点P、B不重合),作y轴的平行线交抛物线于点N,若记点M的横坐标为m,试求线段MN的长L与m之间的函数关系式,画出该函数的示意图,并指出m取何值时,L有最大值,最大值是多少?
【答案】(1) BQ=OQ+AB;(2)见解析;(3)①y=![]() x2﹣2
x2﹣2![]() x+8;②当m取6
x+8;②当m取6![]() 时,L有最大值,且最大值为 2
时,L有最大值,且最大值为 2
【解析】
(1)要写成三个三角形相似的式子,需要先找出相等的对应角,首先由BC∥OA,确定∠CBP=∠BPA>∠QBP,那么三个相似三角形的一组对应角应该是:∠QBP、∠QPO、∠ABP,显然能得出∠QBP=∠ABP、∠OQP=∠BQP,那么过P作BQ的垂线,根据角平分线定理即可判断出OQ、QB、BA三者之间的数量关系.
(2)同(1),先根据图示确定相似三角形的对应角,然后根据三个三角形的对应顶点写出三角形相似的式子;在△BQP、△BPA中,有公共边BP,可确定两者全等,那么BQ=AB,因此确定出∠CBQ的度数,即可确定AB、BC(OA)的比例关系,那么可以从△OQP、△CQB、△ABP这三个相似三角形入手.
(3)①首先结合(1)的解题过程,确定OP的长,进而得出点P的坐标,再利用待定系数法确定抛物线的解析式;
②首先利用待定系数法求出直线BP的解析式,然后根据直线BP、抛物线的解析式,用点M的横坐标表示出点M、N的纵坐标,两点纵坐标的差即为L的函数表达式,再根据函数的性质进行判断即可.
(1)△OPQ和△ABP中,∵∠OPQ+∠APB=90°,且∠APB+∠ABP=90°,
∴∠OPQ=∠ABP;
△BPQ和△ABP中,∵BC∥OA,∴∠APB=∠CBP>∠PBQ,
若两个三角形相似,则:∠PBQ=∠ABP;
∴∠OPQ=∠ABP=∠PBQ
又∵∠O=∠A=∠QPB=90°,
∴△OPQ∽△ABP∽△PBQ.
在△OPQ和△PBQ中,∠OQP=∠PQB,过P作PD⊥BQ于D,则 OQ=QD;
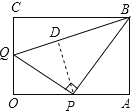
同理,可得:BD=AB,
∴BQ=QD+BD=OQ+AB.
(2)同(1)可确定∠QBP=∠ABP,由图知:∠QPO=∠BPA
∴∠OQP=∠ABP=∠QBP,又∠BQP=∠QOP=∠BAP=90°
∴△OPQ∽△APB∽△QPB.
由(1)的结论知:∠OQP=∠QBC=∠QBP=∠ABP,且∠ABC=90°,
∴∠QBC=30°,则 BQ:CB=2:![]() =2
=2![]() :3;
:3;
由△QPB∽△APB,且BP=BP,所以△QPB≌△APB,得:AB=BQ;
∴AB:BC=2![]() :3,即 AB:OA=2
:3,即 AB:OA=2![]() :3.
:3.
(3)①由(1)的解答过程知:若△OPQ与△PAB和△QPB相似,则必须满足的条件是∠QPB=90゜;
此时∠OQP=∠BQP、∠QBP=∠ABP,由(1)题图可知:OP=AP=PD;
∴OP=AP=![]() OA=4
OA=4![]() ,即 P(4
,即 P(4![]() ,0);
,0);
设抛物线的解析式为:y=a(x﹣4![]() )2,代入点B(8
)2,代入点B(8![]() ,8),得:
,8),得:
a(8![]() ﹣4
﹣4![]() )2=8,解得 a=
)2=8,解得 a=![]()
∴抛物线的解析式为:y=![]() (x﹣4
(x﹣4![]() )2=
)2=![]() x2﹣2
x2﹣2![]() x+8.
x+8.
②设直线BP的解析式为:y=kx+b,代入B(8![]() ,8)、P(4
,8)、P(4![]() ,0),得:
,0),得:
![]() ,解得
,解得 ![]()
∴直线BP:y=![]() x﹣8.
x﹣8.
已知点M的横坐标为m,则 M(m,![]() m﹣8)、N(m,
m﹣8)、N(m,![]() m2﹣2
m2﹣2![]() m+8),则有:
m+8),则有:
MN的长:L=![]() m﹣8﹣(
m﹣8﹣(![]() m2﹣2
m2﹣2![]() m+8)=﹣
m+8)=﹣![]() m2+3
m2+3![]() m﹣16(4
m﹣16(4![]() <m<8
<m<8![]() )(如右图)
)(如右图)
配方,得:L=﹣![]() (m2﹣12
(m2﹣12![]() m+72)+2=﹣
m+72)+2=﹣![]() (m﹣6
(m﹣6![]() )2+2,
)2+2,
∴当m取6![]() 时,L有最大值,且最大值为 2.
时,L有最大值,且最大值为 2.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案科目:初中数学 来源: 题型:
【题目】在“书香八桂,阅读圆梦”读书活动中,某中学设置了书法、国学诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
(1)请求出九(2)全班人数;
(2)请把折线统计图补充完整;
(3)南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
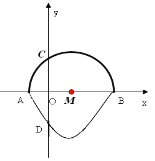
【题目】我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”,如果一条直线与“蛋圆”只有一个交点,那么这条直线叫做“蛋圆”的切线。如图,点A、B、C、D分别是“蛋圆”与坐标轴的交点,点D的坐标为(0,-3)AB为半圆直径,半圆圆心M(1,0),半径为2,则经过点D的“蛋圆”的切线的解析式为__________________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在四边形ABCD中,点E、F是对角线BD上的两点,且BE=FD.
(1)若四边形AECF是平行四边形,求证:四边形ABCD是平行四边形;
(2)若四边形AECF是菱形,那么四边形ABCD也是菱形吗?为什么?
(3)若四边形AECF是矩形,试判断四边形ABCD是否为矩形,不必写理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
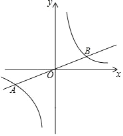
【题目】如图,在平面直角坐标系xOy中,已知正比例函数y=![]() 的图象与反比例函数y=
的图象与反比例函数y=![]() 的图象交于A(a,﹣2),B两点.
的图象交于A(a,﹣2),B两点.
(1)反比例函数的解析式为 ,点B的坐标为 ;
(2)观察图象,直接写出![]() ﹣
﹣![]() <0的解集.
<0的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家发现:课堂上,学生对概念的接受能力s与提出概念的时间t(单位:min)之间近似满足函数关系s=at2+bt+c(a≠0),s值越大,表示接受能力越强.如图记录了学生学习某概念时t与s的三组数据,根据上述函数模型和数据,可推断出当学生接受能力最强时,提出概念的时间为( )
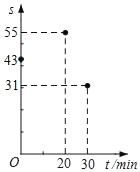
A. 8min B. 13min C. 20min D. 25min
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,将边AB所在直线绕点A逆时针旋转一个角度α得到直线AM,过点C作CE⊥AM,垂足为E,连接BE.
(1)当0°<α<45°时,设AM交BC于点F,
①如图1,若α=35°,则∠BCE= °;
②如图2,用等式表示线段AE,BE,CE之间的数量关系,并证明;
(2)当45°<α<90°时(如图3),请直接用等式表示线段AE,BE,CE之间的数量关系.
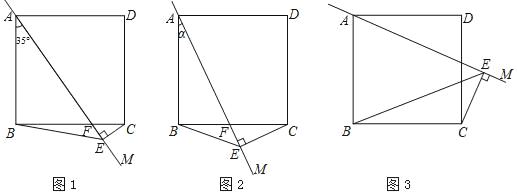
查看答案和解析>>
科目:初中数学 来源: 题型:
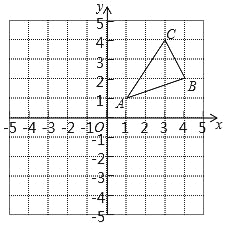
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1)请画出△ABC绕O点逆时针旋转90°得到△A1B1C1,请画出△A1B1C1.
(2)在x轴上求作一点P,使△PA1C1的周长最小,并直接写出P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
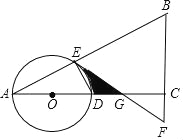
【题目】如图,在△ABC中,∠ACB=90°,O是边AC上一点,以O为圆心,以OA为半径的圆分别交AB、AC于点E、D,在BC的延长线上取点F,使得BF=EF.
(1)判断直线EF与⊙O的位置关系,并说明理由;
(2)若∠A=30°,求证:DG=![]() DA;
DA;
(3)若∠A=30°,且图中阴影部分的面积等于2![]() ,求⊙O的半径的长.
,求⊙O的半径的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com