
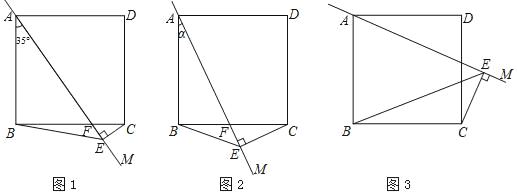
ЁОЬтФПЁПе§ЗНаЮABCDжаЃЌНЋБпABЫљдкжБЯпШЦЕуAФцЪБеыа§зЊвЛИіНЧЖШІСЕУЕНжБЯпAMЃЌЙ§ЕуCзїCEЁЭAMЃЌДЙзуЮЊEЃЌСЌНгBEЃЎ
ЃЈ1ЃЉЕБ0ЁуЃМІСЃМ45ЁуЪБЃЌЩшAMНЛBCгкЕуFЃЌ
ЂйШчЭМ1ЃЌШєІСЃН35ЁуЃЌдђЁЯBCEЃНЁЁ ЁЁЁуЃЛ
ЂкШчЭМ2ЃЌгУЕШЪНБэЪОЯпЖЮAEЃЌBEЃЌCEжЎМфЕФЪ§СПЙиЯЕЃЌВЂжЄУїЃЛ
ЃЈ2ЃЉЕБ45ЁуЃМІСЃМ90ЁуЪБЃЈШчЭМ3ЃЉЃЌЧыжБНггУЕШЪНБэЪОЯпЖЮAEЃЌBEЃЌCEжЎМфЕФЪ§СПЙиЯЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй35ЃЛЂкAEЃНCE+![]() BEЃЎжЄУїМћНтЮіЃЛЃЈ2ЃЉAE+CEЃН
BEЃЎжЄУїМћНтЮіЃЛЃЈ2ЃЉAE+CEЃН![]() BEЃЎРэгЩМћНтЮі.
BEЃЎРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉЂйЫФБпаЮABCDЪЧе§ЗНаЮЭЈЙ§НЧЕФЙиЯЕЧѓГіЁЯAFBЧвCEЁЭAMЃЌМДПЩЧѓГіЁЯBCE.
ЂкЙ§ЕуBзїBGЁЭBEЃЌНЛAMгкЕуGЃЌгЩЂйжаЫФБпаЮABCDЪЧе§ЗНаЮвзЕУЁЯABGЃНЁЯCBEЃЌдйЭЈЙ§жБНЧШ§НЧаЮФкНЧКЭДњЛЛМДПЩЕУЕНЁЯІСЃНЁЯBCEЃЌвзЕУЁїABGЁеЁїCBEЃЈASAЃЉЃЌдкЭЈЙ§ЙДЙЩЖЈРэМДПЩЕУГіAEЃЋCEЃН![]() BE.
BE.
ЃЈ2ЃЉЙ§ЕуBзїBGЁЭBEЃЌНЛAMгкЕуGЃЌгЩЃЈ1ЃЉжаЕУЕНЁЯABGЃНЁЯCBEЃЌдйЭЈЙ§жБНЧШ§НЧаЮФкНЧКЭДњЛЛМДПЩЕУЕНЁЯDAHЃНЁЯDCEЃЌбгГЄDAНЛBGгкNЃЌвзЕУЁЯBAGЃНЁЯBCEЃЌМДПЩЕУЕНЁїABGЁеЁїCBEЃЈASAЃЉЃЌдйЭЈЙ§ЙДЙЩЖЈРэGEЃН![]() BEЃЌЕШСПДњЛЛМДПЩЕУГіAEЃЌBEЃЌCEжЎМфЕФЪ§СПЙиЯЕ.
BEЃЌЕШСПДњЛЛМДПЩЕУГіAEЃЌBEЃЌCEжЎМфЕФЪ§СПЙиЯЕ.
ЃЈ1ЃЉЂйЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌЁрЁЯABCЃН90ЁуЃЌ
ЁпЁЯBAFЃН35ЁуЃЌ
ЁрЁЯAFBЃН90ЁуЉЁЯBAFЃН55ЁуЃЌ
ЁрЁЯCFEЃНЁЯAFBЃН55ЁуЃЌ
ЁпCEЁЭAMЃЌ
ЁрЁЯCEFЃН90ЁуЃЌ
ЁрЁЯECFЃН90ЁуЉЁЯCFEЃН35ЁуЃЌ
МДЃКЁЯBCEЃН35ЁуЃЌ
ЙЪД№АИЮЊЃК35ЃЛ
ЂкAEЃНCEЃЋ![]() BEЃЎ
BEЃЎ
жЄУїЃКШчЭМ2ЃЌЙ§ЕуBзїBGЁЭBEЃЌНЛAMгкЕуGЃЌ
ЁрЁЯGBEЃНЁЯGBCЃЋЁЯCBEЃН90ЁуЃЎ
ЁпЫФБпаЮABCDЮЊе§ЗНаЮЃЌ
ЁрABЃНBCЃЌЁЯABCЃНЁЯABGЃЋЁЯGBCЃН90ЁуЃЌ
ЁрЁЯABGЃНЁЯCBEЃЎ
ЁпЁЯABCЃН90ЁуЃЌ
ЁрЁЯІСЃЋЁЯAFBЃН90ЁуЃЌ
ЁпЁЯCFEЃНЁЯAFBЃЌ
ЁрЁЯІСЃЋЁЯCFEЃН90ЁуЃЌ
ЁпЁЯCEFЃН90ЁуЃЌ
ЁрЁЯBCEЃЋЁЯCFEЃН90ЁуЃЌ
ЁрЁЯІСЃНЁЯBCEЃЎ
дкЁїABGКЭЁїCBEжаЃЌ
ЁЯABGЃНЁЯCBEЃЌABЃНBCЃЌЁЯІСЃНЁЯBCEЃЌ
ЁрЁїABGЁеЁїCBEЃЈASAЃЉЃЌ
ЁрAGЃНCEЃЌBGЃНBEЃЎ
ЁпдкRtЁїBEGжаЃЌBGЃНBEЃЌ
ЁрGEЃН![]() BEЃЌ
BEЃЌ
ЁрAEЃНAGЃЋGEЃНCEЃЋ![]() BEЃЎ
BEЃЎ
ЃЈ2ЃЉРэгЩЃКШчЭМ3ЃЌЙ§ЕуBзїBGЁЭBEЃЌНЛAMгкЕуGЃЌ
ЁрЁЯGBEЃНЁЯGBAЃЋЁЯABEЃН90ЁуЃЎ
ЁпЫФБпаЮABCDЮЊе§ЗНаЮЃЌ
ЁрABЃНBCЃЌЁЯDЃНЁЯABCЃНЁЯABEЃЋЁЯEBCЃН90ЁуЃЌ
ЁрЁЯABGЃНЁЯCBEЃЎ
ЁпЁЯDЃН90ЁуЃЌ
ЁрЁЯDAHЃЋЁЯAHDЃН90ЁуЃЌ
ЁпЁЯAHDЃНЁЯCHEЃЌ
ЁрЁЯDAHЃЋЁЯCHEЃН90ЁуЃЌ
ЁпЁЯCEAЃН90ЁуЃЌ
ЁрЁЯDCEЃЋЁЯCHEЃН90ЁуЃЌ
ЁрЁЯDAHЃНЁЯDCEЃЎ
бгГЄDAНЛBGгкNЃЌ
ЁпЁЯNAGЃНЁЯDAHЃЌЁрЁЯNAGЃНЁЯDCEЃЌ
ЁрЁЯNAGЃЋ90ЁуЃНЁЯDCEЃЋ90ЁуЃЌ
ЁрЁЯBAGЃНЁЯBCE
дкЁїABGКЭЁїCBEжаЃЌ
ЁЯABGЃНЁЯCBEЃЌABЃНBCЃЌЁЯBAGЃНЁЯBCEЃЌ
ЁрЁїABGЁеЁїCBEЃЈASAЃЉЃЌ
ЁрAGЃНCEЃЌBGЃНBEЃЎ
ЁпдкRtЁїBEGжаЃЌBGЃНBEЃЌ
ЁрGEЃН![]() BEЃЌ
BEЃЌ
ЁрAEЃНGEЉAGЃН![]() BEЉCEЃЎ
BEЉCEЃЎ
МДЃКAEЃЋCEЃН![]() BEЃЎ
BEЃЎ



 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
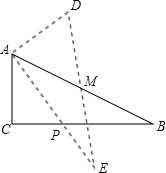
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯC=90ЁуЃЌAB=10ЃЌcosB=![]() ЃЌЕуMЪЧABБпЕФжаЕуЃЌНЋЁїABCШЦзХЕуMа§зЊЃЌЪЙЕуCгыЕуAжиКЯЃЌЕуAгыЕуDжиКЯЃЌЕуBгыЕуEжиКЯЃЌЕУЕНЁїDEAЃЌЧвAEНЛCBгкЕуPЃЌФЧУДЯпЖЮCPЕФГЄЪЧ__________ЃЎ
ЃЌЕуMЪЧABБпЕФжаЕуЃЌНЋЁїABCШЦзХЕуMа§зЊЃЌЪЙЕуCгыЕуAжиКЯЃЌЕуAгыЕуDжиКЯЃЌЕуBгыЕуEжиКЯЃЌЕУЕНЁїDEAЃЌЧвAEНЛCBгкЕуPЃЌФЧУДЯпЖЮCPЕФГЄЪЧ__________ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЦЗЕФНјМлЮЊУПМў30дЊЃЌЪлМлЮЊУПМў40дЊЃЌУПжмПЩТєГі180МўЃЛШчЙћУПМўЩЬЦЗЕФЪлМлУПЩЯеЧ1дЊЃЌдђУПжмОЭЛсЩйТєГі5МўЃЌЕЋУПМўЪлМлВЛФмИпгк50дЊЃЌЩшУПМўЩЬЦЗЕФЪлМлЩЯеЧxдЊЃЈxЮЊећЪ§ЃЉЃЌУПжмЕФЯњЪлРћШѓЮЊyдЊЃЎ
ЃЈ1ЃЉЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂжБНгаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉУПМўЩЬЦЗЕФЪлМлЮЊЖрЩйдЊЪБЃЌУПжмПЩЛёЕУзюДѓРћШѓЃПзюДѓРћШѓЪЧЖрЩйЃП
ЃЈ3ЃЉУПМўЩЬЦЗЕФЪлМлЖЈЮЊЖрЩйдЊЪБЃЌУПжмЕФРћШѓЧЁКУЪЧ2145дЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
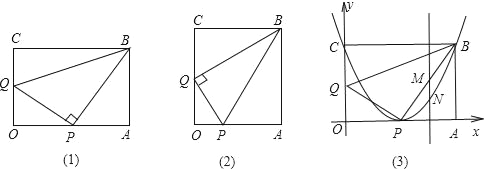
ЁОЬтФПЁПШчЭМЃЌвбжЊОиаЮOABCЃЌЕуPдкБпOAЩЯЃЈВЛгыЖЫЕужиКЯЃЉЃЌЕуQдкБпCOЩЯЃЈВЛгыЖЫЕужиКЯЃЉЃЎ
ЃЈ1ЃЉШчЭМЃЈ1ЃЉЃЌШєЁЯBPQЃН90ЁуЃЌЧвЁїOPQгыЁїPABКЭЁїQPBЯрЫЦЃЌЧыаДГіБэЪОетШ§ИіШ§НЧаЮЯрЫЦЕФЪНзгЃЌВЂЬНОПДЫЪБЯпЖЮOQЁЂQBЁЂBAжЎМфЕФЪ§СПЙиЯЕЃЎ
ЃЈ2ЃЉШєЁЯPQBЃН90ЁуЃЌЧвЁїOPQгыЁїPABЁЂЁїQPBЖМЯрЫЦЃЌШчЭМЃЈ2ЃЉЃЌЧыжиаТаДГіБэЪОетШ§ИіШ§НЧаЮЯрЫЦЕФЪНзгЃЌВЂжЄУїABЃКOAЃН2![]() ЃК3ЃЎ
ЃК3ЃЎ
ЃЈ3ЃЉдкЃЈ1ЃЉжаЃЌШєOAЃН8![]() ЃЌOCЃН8ЃЌOPЃН
ЃЌOCЃН8ЃЌOPЃН![]() CQЃЎвдОиаЮOABCЕФСНБпOAЁЂOCЫљдкЕФжБЯпЗжБ№ЮЊxжсКЭyжсЃЌНЈСЂЦНУцжБНЧзјБъЯЕЃЌШчЭМЃЈ3ЃЉЃЌШєФГХзЮяЯпЖЅЕуЮЊPЃЌЕуBдкХзЮяЯпЩЯЃЎ
CQЃЎвдОиаЮOABCЕФСНБпOAЁЂOCЫљдкЕФжБЯпЗжБ№ЮЊxжсКЭyжсЃЌНЈСЂЦНУцжБНЧзјБъЯЕЃЌШчЭМЃЈ3ЃЉЃЌШєФГХзЮяЯпЖЅЕуЮЊPЃЌЕуBдкХзЮяЯпЩЯЃЎ
ЂйЧѓДЫХзЮяЯпЕФНтЮіЪНЃЎ
ЂкЙ§ЯпЖЮBPЩЯвЛЖЏЕуMЃЈЕуMгыЕуPЁЂBВЛжиКЯЃЉЃЌзїyжсЕФЦНааЯпНЛХзЮяЯпгкЕуNЃЌШєМЧЕуMЕФКсзјБъЮЊmЃЌЪдЧѓЯпЖЮMNЕФГЄLгыmжЎМфЕФКЏЪ§ЙиЯЕЪНЃЌЛГіИУКЏЪ§ЕФЪОвтЭМЃЌВЂжИГіmШЁКЮжЕЪБЃЌLгазюДѓжЕЃЌзюДѓжЕЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
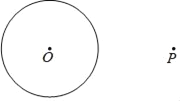
ЁОЬтФПЁПЯТУцЪЧаЁмПЩшМЦЕФЁАЙ§дВЭтвЛЕузївбжЊдВЕФЧаЯпЁБЕФГпЙцзїЭМЙ§ГЬЃЎ
вбжЊЃКЁбOМАЁбOЭтвЛЕуPЃЎ
ЧѓзїЃКЁбOЕФвЛЬѕЧаЯпЃЌЪЙетЬѕЧаЯпОЙ§ЕуPЃЎ
зїЗЈЃКЂйСЌНгOPЃЌзїOPЕФДЙжБЦНЗжЯпlЃЌ
НЛOPгкЕуAЃЛ
ЂквдAЮЊдВаФЃЌAOЮЊАыОЖзїдВЃЌ
НЛЁбOгкЕуMЃЛ
ЂлзїжБЯпPMЃЌдђжБЯпPMМДЮЊЁбOЕФЧаЯпЃЎ
ИљОнаЁмПЩшМЦЕФГпЙцзїЭМЙ§ГЬЃЌ
ЃЈ1ЃЉЪЙгУжБГпКЭдВЙцЃЌВЙШЋЭМаЮЃЛЃЈБЃСєзїЭМКлМЃЃЉ
ЃЈ2ЃЉЭъГЩЯТУцЕФжЄУїЃК
жЄУїЃКСЌНгOMЃЌ
гЩзїЭМПЩжЊЃЌAЮЊOPжаЕуЃЌ
ЁрOPЮЊЁбAжБОЖЃЌ
ЁрЁЯOMPЃНЁЁ ЁЁЁуЃЌЃЈЁЁ ЁЁЃЉЃЈЬюЭЦРэЕФвРОнЃЉ
МДOMЁЭPMЃЎ
гжЁпЕуMдкЁбOЩЯЃЌ
ЁрPMЪЧЁбOЕФЧаЯпЃЎЃЈЁЁ ЁЁЃЉЃЈЬюЭЦРэЕФвРОнЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкxжсЕФе§АыжсЩЯвРДЮНиШЁOA1ЃНA1A2ЃНA2A3ЃНA3A4ЃНA4A5ЃЌЙ§ЕуA1ЁЂA2ЁЂA3ЁЂA4ЁЂA5ЗжБ№зїxжсЕФДЙЯпгыЗДБШР§КЏЪ§yЃН![]() ЃЈxЁй0ЃЉЕФЭМЯѓЯрНЛгкЕуP1ЁЂP2ЁЂP3ЁЂP4ЁЂP5ЃЌЕУжБНЧШ§НЧаЮOP1A1ЁЂA1P2A2ЃЌA2P3A3ЃЌA3P4A4ЃЌA4P5A5ЃЌВЂЩшЦфУцЛ§ЗжБ№ЮЊS1ЁЂS2ЁЂS3ЁЂS4ЁЂS5ЃЌдђS10ЃН_____ЃЎЃЈnЁн1ЕФећЪ§ЃЉ
ЃЈxЁй0ЃЉЕФЭМЯѓЯрНЛгкЕуP1ЁЂP2ЁЂP3ЁЂP4ЁЂP5ЃЌЕУжБНЧШ§НЧаЮOP1A1ЁЂA1P2A2ЃЌA2P3A3ЃЌA3P4A4ЃЌA4P5A5ЃЌВЂЩшЦфУцЛ§ЗжБ№ЮЊS1ЁЂS2ЁЂS3ЁЂS4ЁЂS5ЃЌдђS10ЃН_____ЃЎЃЈnЁн1ЕФећЪ§ЃЉ
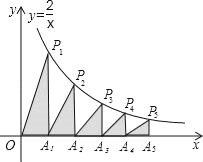
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌOЮЊЯпЖЮABЕФжаЕуЃЌABЃН4cmЃЌP1ЁЂP2ЁЂP3ЁЂP4ЕНЕуOЕФОрРыЗжБ№ЪЧ1cmЁЂ2cmЁЂ2.8cmЁЂ1.7cmЃЌЯТСаЫФЕужаФмгыAЁЂBЙЙГЩжБНЧШ§НЧаЮЕФЖЅЕуЪЧЃЈЁЁЁЁЃЉ
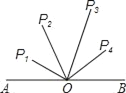
A. P1 B. P2 C. P3 D. P4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвCDЁЭABЃЌДЙзуЮЊHЃЌСЌНсACЃЌЙ§ЛЁBDЩЯвЛЕуEзїEGЁЮACНЛCDЕФбгГЄЯпгкЕуGЃЌСЌНсAEНЛCDгкЕуFЃЌЧвEGЃНFGЃЌСЌНсCEЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїECFЁзЁїGCEЃЛ
ЃЈ2ЃЉЧѓжЄЃКEGЪЧЁбOЕФЧаЯпЃЛ
ЃЈ3ЃЉбгГЄABНЛGEЕФбгГЄЯпгкЕуMЃЌШєtanЁЯGЃН![]() ЃЌAHЃН3ЃЌЧѓEMЕФжЕЃЎ
ЃЌAHЃН3ЃЌЧѓEMЕФжЕЃЎ
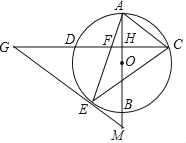
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁЯAOB=90ЁуЃЌOA=90cmЃЌOB=30cmЃЌвЛЛњЦїШЫдкЕуBДІПДМћвЛИіаЁЧђДгЕуAГіЗЂбизХAOЗНЯђдШЫйЙіЯђЕуOЃЌЛњЦїШЫСЂМДДгЕуBГіЗЂЃЌбижБЯпдШЫйЧАНјРЙНиаЁЧђЃЌЧЁКУдкЕуCДІНизЁСЫаЁЧђЃЎШчЙћаЁЧђЙіЖЏЕФЫйЖШгыЛњЦїШЫаазпЕФЫйЖШЯрЕШЃЌФЧУДЛњЦїШЫаазпЕФТЗГЬBCЪЧЖрЩй?

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com