
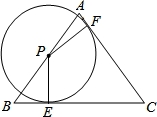
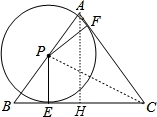
如图,△ABC中AB=AC=5,BC=6,点P在边AB上,以P为圆心的⊙P分别与边AC、BC相切于点E、F,则⊙P的半径PE的长为( )
A.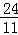 B.2 C.
B.2 C.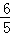 D.
D.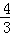
A【考点】切线的性质.
【专题】计算题.
【分析】连结CP,作AH⊥BC于H,如图,设⊙P的半径为r,根据等腰三角形的性质得BH=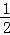 BC=3,则利用勾股定理可计算出AH=4,再根据切线的性质得PE⊥BC,PF⊥AC,利用S△ABC=S△PAC+S△PBC得到
BC=3,则利用勾股定理可计算出AH=4,再根据切线的性质得PE⊥BC,PF⊥AC,利用S△ABC=S△PAC+S△PBC得到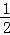 BC×AH=
BC×AH=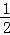 BC×PE+
BC×PE+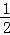 AC×PF,即6×4=6r+5r,然后解方程即可.
AC×PF,即6×4=6r+5r,然后解方程即可.
【解答】解:连结CP,作AH⊥BC于H,如图,设⊙P的半径为r,
∵AB=AC=5,
∴BH=CH=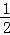 BC=3,
BC=3,
∴AH=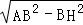 =4,
=4,
∵以P为圆心的⊙P分别与边AC、BC相切于点E、F,
∴PE⊥BC,PF⊥AC,
∵S△ABC=S△PAC+S△PBC,
∴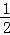 BC×AH=
BC×AH=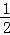 BC×PE+
BC×PE+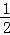 AC×PF,
AC×PF,
即6×4=6r+5r,
∴r=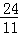 .
.
故选A.
【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.也考查了等腰三角形的性质和三角形面积公式.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
将一枚骰子抛掷两次,第一次出现的点数记为 ,第二次出现的点数记为
,第二次出现的点数记为 ,设点
,设点 (
( ,
, )是反比例函数图象上的点.
)是反比例函数图象上的点.
(1)用列表或树状图的方法列举所有 (
( ,
, )的情况;
)的情况;
(2)分别求出点在反比例函数 和反比例函数
和反比例函数 的图象上的点的概率.
的图象上的点的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
.函数y=-x2-3的图象向上平移2个单位,再向左平移2个单位后,得到的函数是
A.y=-(x+2)2-1 B.y=-(x-2)2-1
C.y=-(x-2)2+1 D.y=-(x+2)2+1
查看答案和解析>>
科目:初中数学 来源: 题型:
已知反比例函数y=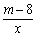 (m为常数)的图象经过点A(-1,6).
(m为常数)的图象经过点A(-1,6).
(1)求m的值;
(2)如图,过点A作直线AC与函数y=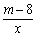 的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.
的图象交于点B,与x轴交于点C,且AB=2BC,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
九年级(1)班数学活动选出甲、乙两组各10名学生,进行趣味数学答题比赛,共10题,答对题数统计如表一:
(表一)
| 答对题数 | 5 | 6 | 7 | 8 | 9 | 10 |
| 甲组 | 1 | 0 | 1 | 5 | 2 | 1 |
| 乙组 | 0 | 0 | 4 | 3 | 2 | 1 |
(表二)
| 平均数 | 众数 | 中位数 | 方差 | |
| 甲组 | 8 | 8 | 8 | 1.6 |
| 乙 | 8 | __________ | __________ | __________ |
(1)根据表一中统计的数据,完成表二;
(2)请你从平均数和方差的角度分析,哪组的成绩更好些?
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的布袋里装有红、黄、绿三种颜色的球(除颜色不同,其它均无任何区别),其中红球2个,黄球1个,绿球1个.
(1)求从袋中任意摸出一个球是红球的概率;
(2)第一次从袋中任意摸出一个球,记下颜色后放回袋中,第二次再摸出一个球记下颜色,请用画树状图或列表的方法求两次都摸到红球的概率(两个红球分别记作红1、红2).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com