
【题目】某水果批发市场规定,批发苹果不少于![]() 时,批发价为5元/
时,批发价为5元/![]() .小王携带现金4000元到这市场采购苹果,并以批发价买进.
.小王携带现金4000元到这市场采购苹果,并以批发价买进.
(Ⅰ)根据题意,填表:
购买数量 |
|
|
|
|
花费 |
|
| ||
剩余现金 |
|
|
(Ⅱ)设购买的苹果为![]() ,小王付款后还剩余现金
,小王付款后还剩余现金![]() 元.求
元.求![]() 关于
关于![]() 的函数解析式,并指出自变量
的函数解析式,并指出自变量![]() 的取值范围;
的取值范围;
(Ⅲ)根据题意填空:若小王剩余现金为700元,则他购买__________![]() 的苹果.
的苹果.
【答案】(Ⅰ)500,1500;3500,2500;(Ⅱ)![]() ,
,![]() ;(Ⅲ)660.
;(Ⅲ)660.
【解析】
(Ⅰ)根据:数量×单价=花费,剩余现金=4000-花费,计算即可;
(Ⅱ)剩余现金=总现金数-购买苹果费用,根据购买千克数应不少于100以及剩余现金为非负数可得自变量的取值;
(Ⅲ)把y=700代入(Ⅱ)得到关系式,计算即可.
解:(Ⅰ)100×5=500元,4000-500=3500元;
300×5=1500元,4000-1500=2500元;
故答案为:500,1500;3500,2500;
(Ⅱ)由题意得![]() .
.
由![]() ,得
,得![]() .
.
又![]() ,
,
∴自变量![]() 的取值范围是
的取值范围是![]() ,
,
∴![]() (
(![]() );
);
(Ⅲ)当y=700时,
4000-5x=700,
∴x=660.
故答案为:660.


科目:初中数学 来源: 题型:
【题目】目前“校园手机”现象越来越受到社会关注,针对这种现象,某校九年级数学兴趣小组的同学随机调查了若干名家长对“中学生带手机的”的态度(态度分为:A.无所谓;B.基本赞成;C.赞成;D.反对).并将调查结果绘制成频数折线统计图1和扇形统计图2(不完整).请根据图中提供的信息,解答下列问题:
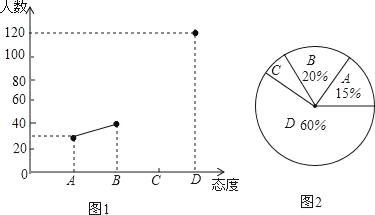
(1)此次抽样调查中,共调查了多少名中学生家长;
(2)求出图2中扇形C所对的圆心角的度数,并将图1补充完整;
(3)在此次调查活动中,初三(1)班有A1、A2两位家长对中学生带手机持反对态度,初三(2)班有B1、B2两位学生家长对中学生带手机也持反对态度,现从这4位家长中选2位家长参加学校组织的家校活动,用列表法或画树状图的方法求出选出的2人来自不同班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )
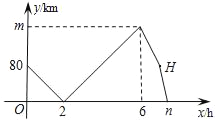
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一条公路旁依次有A,B,C三个村庄,甲乙两人骑自行车分别从A村、B村同时出发前往C村,甲乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:①A,B两村相距10km;②出发1.25h后两人相遇:③甲每小时比乙多骑行8km;④相遇后,乙又骑行了15min时两人相距2km.其中正确的有______.(填序号)
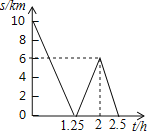
查看答案和解析>>
科目:初中数学 来源: 题型:
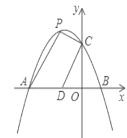
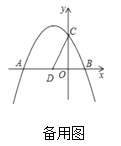
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .已知点
.已知点![]() 的坐标为
的坐标为![]() ,点
,点![]() 为第二象限内抛物线上的一个动点,连接
为第二象限内抛物线上的一个动点,连接![]() 、
、![]() 、
、![]() .
.
(1)求这个抛物线的表达式.
(2)当四边形![]() 面积等于4时,求点
面积等于4时,求点![]() 的坐标.
的坐标.
(3)①点![]() 在平面内,当
在平面内,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,直接写出满足条件的所有点
为斜边的等腰直角三角形时,直接写出满足条件的所有点![]() 的坐标;
的坐标;
②在①的条件下,点![]() 在抛物线对称轴上,当
在抛物线对称轴上,当![]() 时,直接写出满足条件的所有点
时,直接写出满足条件的所有点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
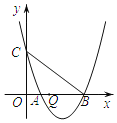
【题目】如图,抛物线y=![]() x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
x+3与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,点Q是线段OB上一动点,连接BC,点M在线段BC上,且使△BQM为直角三角形的同时△CQM为等腰三角形,则此时点Q的横坐标为( )
A.![]() 或
或![]() B.
B.![]() 或
或![]() C.
C.![]() 或
或![]() D.
D.![]() 或
或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
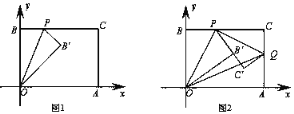
【题目】已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(4,0),点B(0,3),点P为BC边上的动点(点P不与点B、C重合),经过点O、P折叠该纸片,得点B′和折痕OP.设BP=t.
(1)如图1,当∠BOP=30°时,求点P的坐标;
(2)如图2,经过点P再次折叠纸片,使点C落在直线PB′上,得点C′和折痕PQ,设AQ=m,试用含有t的式子表示m;
(3)在(2)的条件下,连接OQ,当OQ取得最小值时,求点Q的坐标;
(4)在(2)的条件下,点C′能否落在边OA上?如果能,直接写出点P的坐标;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图抛物线![]() 的开口向下与
的开口向下与![]() 轴交于点
轴交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是抛物线上一个动点(不与点
是抛物线上一个动点(不与点![]() 重合)
重合)

(1)求抛物线的解析式;
(2)当点![]() 是抛物线上一个动点,若
是抛物线上一个动点,若![]() 的面积为12,求点
的面积为12,求点![]() 的坐标;
的坐标;
(3)如图2,抛物线的顶点为![]() ,在抛物线上是否存在点
,在抛物线上是否存在点![]() ,使得
,使得![]() ,若存在请直接写出点
,若存在请直接写出点![]() 的坐标;若不存在请说明理由.
的坐标;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是
是![]() 所对弦
所对弦![]() 上一动点,点
上一动点,点![]() 在
在![]() 的延长线上,过点
的延长线上,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,已知
,已知![]() ,
,![]() ,设
,设![]() ,
,![]() 两点间的距离为
两点间的距离为![]() ,
,![]() 的面积为
的面积为![]() .(当点
.(当点![]() 与点
与点![]() ,
,![]() 重合时,
重合时,![]() 的值为0.)
的值为0.)

小亮根据学习函数的经验,对函数![]() 随自变量
随自变量![]() 的变化而变化的规律进行了探究.
的变化而变化的规律进行了探究.
下面是小亮的探究过程,请补充完整:
(1)通过取点、画图、测量,得到了![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 0 | 4.47 | 7.07 | 9.00 | 8.94 | 0 |
(2)在平面直角坐标系中,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
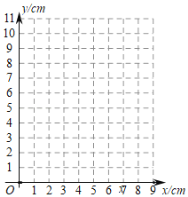
(3)结合画出的函数图象,解决问题:当![]() 的面积为
的面积为![]() 时,
时,![]() 的长度约为
的长度约为 ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com