
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分线交BC于E,连接DE.
(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.

【答案】见解析
【解析】试题分析:(1)根据题中条件可证明△AOB≌△AOD,得到OD=OB,可证点D在△ABE的外接圆上;
(2)根据∠C=90°,可得∠CED+∠CDE=90°;利用∠ODE=∠DEC,可知∠ODC=∠CDE+∠ODE=∠CDE+∠CED=90°,即CD与△ABE的外接圆相切.
试题解析:证明:(1)∵∠B=90°,∴AE是△ABE外接圆的直径.
取AE的中点O,则O为圆心,连接OB、OD.
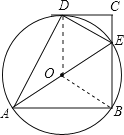
在△AOB和△AOD中,∵AB=AD,∠BAC=∠DAO,AO=AO,∴△AOB≌△AOD.∴OD=OB,∴点D在△ABE的外接圆上.
(2)直线CD与△ABE的外接圆相切.
理由:∵AB∥CD,∠B=90°.∴∠C=90°,∴∠CED+∠CDE=90°.
又∵OE=OD,∴∠ODE=∠OED.
又∠AED=∠CED,∴∠ODE=∠DEC,∴∠ODC=∠CDE+∠ODE=∠CDE+∠CED=90°,∴CD与△ABE的外接圆相切.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,
,![]() ,
,![]() ,点E在线段AB上,
,点E在线段AB上,![]() ,点F在直线AD上,
,点F在直线AD上,![]() .
.
![]() 若
若![]() ,求
,求![]() 的度数;
的度数;
![]() 找出图中与
找出图中与![]() 相等的角,并说明理由;
相等的角,并说明理由;
![]() 在
在![]() 的条件下,点
的条件下,点![]() 不与点B、H重合
不与点B、H重合![]() 从点B出发,沿射线BG的方向移动,其他条件不变,请直接写出
从点B出发,沿射线BG的方向移动,其他条件不变,请直接写出![]() 的度数
的度数![]() 不必说明理由
不必说明理由![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店需要购进甲、乙两种商品共180件,其进价和售价如表:(注:获利=售价-进价)
甲 | 乙 | |
进价(元/件) | 14 | 35 |
售价(元/件) | 20 | 43 |
(1)若商店计划销售完这批商品后能获利1240元,问甲、乙两种商品应分别购进多少件?
(2)若商店计划投入资金少于5040元,且销售完这批商品后获利多于1312元,请问有哪几种购货方案?并直接写出其中获利最大的购货方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0, ![]() ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
(1)求A、B两点的坐标;
(2)求经过点A,C,B的抛物线C1的函数表达式.
(3)探究“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC面积的最大值;若不存在,请说明理由.
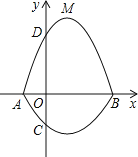
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个三位数![]() ,如果
,如果![]() 满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”
满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”![]() 的各个数位上的数字之和记为
的各个数位上的数字之和记为![]() . 例如
. 例如![]() 时,
时,![]() .
.
(1)对于“相异数”![]() ,若
,若![]() ,请你写出一个
,请你写出一个![]() 的值;
的值;
(2)若![]() 都是“相异数”,其中
都是“相异数”,其中![]() ,
,![]() (
(![]() ,
,![]() 都是正整数),规定:
都是正整数),规定:![]() ,当
,当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个动点P在平面直角坐标系中按箭头所示方向作折线运动,即第一次从原点运动到(1,1),第二次从(1,1)运动到(2,0),第三次从(2,0)运动到(3,2),第四次从(3,2)运动到(4,0),第五次从(4,0)运动到(5,1),……,按这样的运动规律,经过第2019次运动后,动点P的坐标是___________
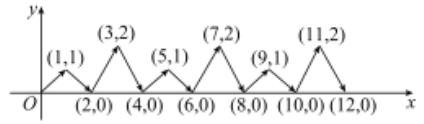
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.
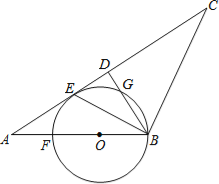
(1)判断直线AC与⊙O的位置关系,并说明理由;
(2)当BD=6,AB=10时,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com