
【题目】如图所示,在平面直角坐标系中,A、B为x轴上两点,C、D为y轴上两点,经过点A,C,B的抛物线的一部分C1与经过点A,D,B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0, ![]() ),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
),点M是抛物线C2:y=mx2-2mx-3m(m<0)的顶点:
(1)求A、B两点的坐标;
(2)求经过点A,C,B的抛物线C1的函数表达式.
(3)探究“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出点P的坐标及△PBC面积的最大值;若不存在,请说明理由.
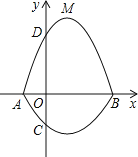
【答案】(1)A(-1,0),B(3,0);(2)![]() ;(3)当P点坐标为(
;(3)当P点坐标为(![]() ,
, ![]() )时,
)时, ![]() 有最大值,
有最大值, ![]() .
.
【解析】试题分析:(1)把抛物线解析整理,令y=0可求得x的值,则可求得A、B的坐标;
(2)由A、B、C的坐标,利用待定系数法可求得经过点A、B、C的抛物线解析式;
(3)连接BC、过点P作PQ∥y轴,交BC于点Q,由B、C的坐标可求得直线BC的解析式,则可设出P点坐标,从而表示出Q点坐标,则可求得PQ的长,从而用P点坐标表示出△PBC的面积,利用二次函数的性质可求得P点坐标和△PBC面积的最大值.
试题解析:解:(1)∵y=mx2-2mx-3m=m(x-3)(x+1),且m≠0,
∴当y=0时,可得m(x-3)(x+1)=0,解得x1=-1,x2=3,
∴A(-1,0),B(3,0);
(2)设过A、B、C三点的抛物线解析式为y=ax2+bx+c,
则有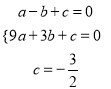 ,解得
,解得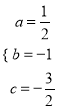 ,
,
∴抛物线C1解析式为![]() ;
;
(3)如图,过点P作PQ∥y轴,交BC于Q,
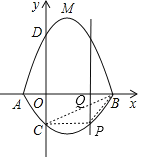
设直线BC解析式为y=kx+s,则有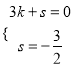 ,解得
,解得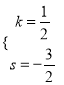 ,
,
∴ 直线BC的解析式为![]() ,
,
设P(x, ![]() ),则Q(x,
),则Q(x, ![]() ),
),
∴ PQ= ![]() ,
,
∴ S△PBC=![]() PQOB=
PQOB=![]() ×(
×(![]() x2+
x2+![]() x)×3=
x)×3=![]() (x
(x![]() )2+
)2+![]() ,
,
∵![]() <0,
<0,
∴ 当x=![]() 时,S△PBC有最大值,S最大=
时,S△PBC有最大值,S最大=![]() ,此时P点纵坐标为
,此时P点纵坐标为![]() ,
,
∴ 此时P点坐标为(![]() ,
, ![]() ).
).


科目:初中数学 来源: 题型:
【题目】(1)如图,∠1=75°,∠2=105°,∠C=∠D.判断 ∠A与 ∠F的大小关系,并说明理由.

(2)对于某些数学问题,灵活运用整体思想,可以化难为易.在解二元一次方程组时,就可以运用整体代入法:如解方程组: .
.
解:把②代入①得,![]() 解得
解得![]() 把
把![]() 代入②得,
代入②得,![]()
所以方程组的解为 ![]()
请用同样的方法解方程组: .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=4,BC=6,E是BC边的中点,点P在线段AD上,过P作PF⊥AE于F,设PA=x.
(1)求证:△PFA∽△ABE;
(2)当点P在线段AD上运动时,设PA=x,是否存在实数x,使得以点P,F,E为顶点的三角形也与△ABE相似?若存在,请求出x的值;若不存在,请说明理由;
(3)探究:当以D为圆心,DP为半径的⊙D与线段AE只有一个公共点时,请直接写出x满足的条件: .

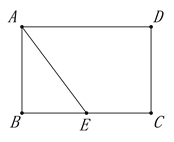
备用图
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的周长为16,D, E,F分别为AB, BC,AC的中点,M,N,P分别为DE, EF,DF的中点,则△MNP的周长为____;如果△ABC,△DEF,△MNP分别为第1个,第2个,第3个三角形,按照上述方法继续做三角形,那么第n个三角形的周长是___.
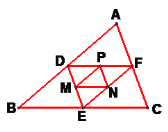
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分线交BC于E,连接DE.
(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
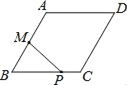
【题目】如图,菱形ABCD中,AB=2,∠B=60°,M为AB的中点.动点P在菱形的边上从点B出发,沿B→C→D的方向运动,到达点D时停止.连接MP,设点P运动的路程为x,MP 2=y,则表示y与x的函数关系的图象大致为( )
A. 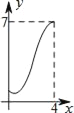 B.
B. 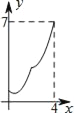 C.
C. 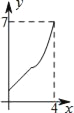 D.
D. 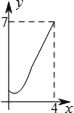
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校举办了一次趣味数学竞赛,满分100分,学生得分均为整数,达到成绩60分及以上为合格,达到90分及以上为优秀,这次竞赛中,甲乙两组学生成绩如下,甲组:30,60,60,60,60,60,70,90,90,100 ;乙组:50,60,60,60,70,70,70,70,80,90.
(1)以上成绩统计分析表中a=______分,b=______分,c=_______分;
组别 | 平均数 | 中位数 | 方差 | 合格率 | 优秀率 |
甲组 | 68分 | a | 376 | 30% | |
乙组 | b | c | 90% |
(2)小亮同学说:这次竞赛我得了70分,在我们小组中属于中游略偏上,观察上面表格判断,小亮可能是甲乙哪个组的学生?并说明理由
(3)计算乙组的方差和优秀率,如果你是该校数学竞赛的教练员,现在需要你选一组同学代表学校参加复赛,你会选择哪一组?并说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客居住,当每个房间每天的定价为180元时,房间会全部住满;当每个房间每天的定价每增加10元时,就会有一个房间空闲.如果游客居住房间,宾馆需对每个房间每天支出20元的各种费用.
(1)若每个房间定价增加40元,则这个宾馆这一天的利润为多少元?
(2)若宾馆某一天获利10640元,则房价定为多少元?
(3)房价定为多少时,宾馆的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下列一段文字,再解答问题:
已知在平面内有两点![]() ,
,![]() ,其两点间的距离公式为
,其两点间的距离公式为![]() ;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为
;同时,当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为![]() 或
或![]() .
.
(1)已知点A(2,4),B(-2,1),则AB=__________;
(2)已知点C,D在平行于y轴的直线上,点C的纵坐标为4,点D的纵坐标为-2,则CD=__________;
(3)已知点P(3,1)和(1)中的点A,B,判断线段PA,PB,AB中哪两条线段的长是相等的?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com