
【题目】如图,O是直线AB上一点,OC为任一条射线,OM平分∠AOC,ON平分∠BOC.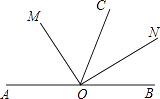
(1)图中与∠AON互补的角有;
(2)猜想∠MON的度数为 , 试说明理由.
【答案】
(1)∠CON、∠BON
(2)解:∠MON=90°,∵ON平分∠BOC,OM平分∠AOC,∴∠CON= ![]() ∠BOC,∠COM=
∠BOC,∠COM= ![]() ∠COA,∴∠MON=
∠COA,∴∠MON= ![]() ∠BOC+
∠BOC+ ![]() ∠COA=90°
∠COA=90°
【解析】解:(1)∵ON平分∠BOC,
∴∠CON=∠BON,
∵∠BON+∠AON=180°,
∴∠CON+∠AON=180°,
∴与∠AON互补的角有∠CON、∠BON,
故答案为:∠CON、∠BON;
(1)当两角之和为180°,则这两个角互补。根据图形可知∠BON和∠AON互补,根据角平分线的定义(ON平分∠BOC),得出∠CON=∠BON,即可得出与∠AON互补的角。
(2)根据角平分线的定义,分别得出∠CON与 ∠BOC,∠COM与 ∠COA的数量关系,再根据∠MON=∠CON+∠COM,即可得出结论。


科目:初中数学 来源: 题型:
【题目】某果园有100颗橙子树,平均每颗树结600个橙子,现准备多种一些橙子树以提高果园产量,但是如果多种树,那么树之间的距离和每一棵树所接受的阳光就会减少.根据经验估计,每多种一棵树,平均每棵树就会少结5个橙子,假设果园多种了x棵橙子树.
(1)直接写出平均每棵树结的橙子个数y(个)与x之间的关系;
(2)果园多种多少棵橙子树时,可使橙子的总产量最大?最大为多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABE和△ADC是△ABC分别沿着AB,AC边翻折180°形成的,若∠1:∠2:∠3=28:5:3,则∠α的度数为( ) 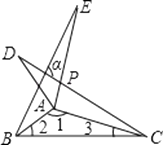
A.80°
B.100°
C.60°
D.45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽像出的几何图形,B,C,E在同一条直线上,连结DC. 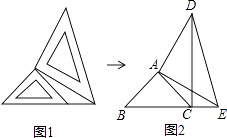
(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的宇母);
(2)证明:DC⊥BE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是用棋子摆成的“H”字,第一个“H”有7个棋子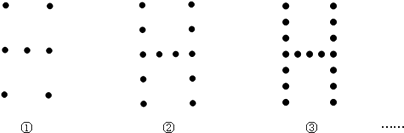
(1)摆成第二个“H”字需要几个棋子?第三个“H”字需要几个棋子?
(2)按这样的规律摆下去,摆成第10个“H”字需要几个棋子,第n个呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ACB中,∠ACB=90°,BC=3,AC=4,在直线BC上找一点P,使得△ABP为以AB为腰的等腰三角形,则PC的长度为 . 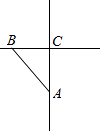
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com