

���� ��1�����á����ڱ��ı��Ρ��Ķ���ֱ���жϼ��ɣ�
��2������ƽ���ı��ε��ж��͡����ڱ��ı��Ρ��Ķ���ֱ���жϼ��ɣ�
��3�����á����ڱ��ı��Ρ��Ķ����ƽ�Ƶ����ʣ���Ӧ�߶�ƽ������ȣ��������������AA��=AB��AA��=A��C�䣬A��C��=BC�䣬BC��=AB���������ۼ��㼴�ɣ�
��� ��1���⣺AB=BC��BC=CD��CD=AD��AD=AB
��2���⣺С��Ľ�����ȷ��
�������£����ı��εĶԽ�����ƽ�֣�
������ı�����ƽ���ı��Σ�
���ı����ǡ����ڱ��ı��Ρ���
������ı�����һ���ڱ���ȣ�
����������ڱ��ı��Ρ������Σ�
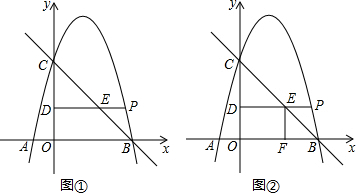
��3���⣺�ɡ�ABC=90�㣬AB=2��BC=1���ã�AC=$\sqrt{5}$��
�߽�Rt��ABCƽ�Ƶõ�Rt��A��B��C�䣬
��BA��=AA�䣬A��B���AB��A��B��=AB=2��B��C��=BC=1��A��C��=AC=$\sqrt{5}$��
��I����ͼ1����AA��=ABʱ��BB��=AA��=AB=2��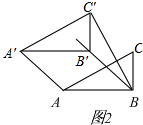
��II����ͼ2����AA��=A��C��ʱ��BB��=AA��=AC��=$\sqrt{5}$��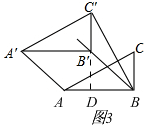
��III����AC��=BC��=$\sqrt{5}$ʱ����ͼ3���ӳ�C��B�佻AB�ڵ�D����C��B���AB
��BB��ƽ�֡�ABC��
���ABB��=$\frac{1}{2}$��ABC=45��
���BB��D=��ABB��=45�㣬
��B��D=BD��
��B��D=BD=x����C��D=x+1��BB��=$\sqrt{2}$x
�߸�����Rt��BC��D�У�BC��2=C��D2+BD2��x2+��x+1��2=5
��ã�x=1��x=-2���������⣬��ȥ��
��BB��=$\sqrt{2}x=\sqrt{2}$��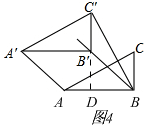
��IV����BC��=AB=2ʱ����ͼ4���루III������ͬ���ɵã�x=$\frac{-1+\sqrt{7}}{2}$��x=$\frac{-1-\sqrt{7}}{2}$��
x=$\frac{-1+\sqrt{7}}{2}$��x=$\frac{-1-\sqrt{7}}{2}$����ȥ��
��BB��=$\sqrt{2}$x=$\frac{-\sqrt{2}+\sqrt{14}}{2}$��
��Ӧƽ��2��$\sqrt{5}$��$\sqrt{2}$��$\frac{-\sqrt{2}+\sqrt{14}}{2}$��
���� �������ı��ε��ۺ��⣬���á����ڱ��ı��Ρ��Ķ��������Ϣ������⣬�漰����ͼ�ε�ƽ�Ƶ����ʣ��ó�BB��=AA�䣬A��B���AB��A��B��=AB=2��B��C��=BC=1��A��C��=AC���ǵ�ƽ���ߵ����ʣ���BB��ƽ�֡�ABC�õ���ABB��=$\frac{1}{2}$��ABC=45�㣬���ɶ���������Ĺؼ������⡰���ڱ��ı��Ρ��Ķ����ǰ���£������ѧ֪ʶ��������



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
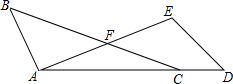 ��ͼ����A��C��D��ͬһ��ֱ���ϣ�BC��AE���ڵ�F��FA=FC����D=
��ͼ����A��C��D��ͬһ��ֱ���ϣ�BC��AE���ڵ�F��FA=FC����D=�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a3•a6=a9 | B�� | ��a2��3=a5 | C�� | 4a3-2a2=2 | D�� | ��3a��2=6a2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com