Question

【题目】（14分）如图，已知抛物线（）与x轴交于点A（1，0）和点B（﹣3，0），与y轴交于点C，且OC=OB．

（1）求此抛物线的解析式；

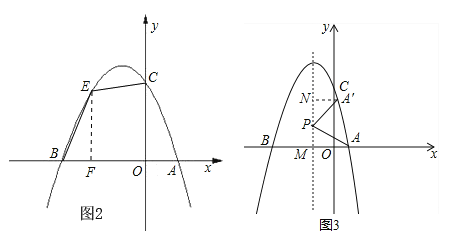
（2）若点E为第二象限抛物线上一动点，连接BE，CE，求四边形BOCE面积的最大值，并求出此时点E的坐标；

（3）点P在抛物线的对称轴上，若线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，求点P的坐标．

Answer 1

【答案】（1）；（2）当a=时，S四边形BOCE最大，且最大值为，此时，点E坐标为（，）；（3）P（﹣1，1）或（﹣1，﹣2）．

【解析】

试题分析：（1）将A、B两点的坐标代入抛物线的解析式中，即可求出二次函数的解析式；

（2）过E作EF⊥x轴于F．设E（a，）（﹣3＜a＜0），则EF=，BF=a+3，OF=﹣a，∴S四边形BOCE==BFEF+（OC+EF）OF =，配方即可得出结论，当a=时，=大，即可得到点E的坐标；

（3）由P在抛物线的对称轴上，设出P坐标为（﹣2，m），如图所示，过A′作A′N⊥对称轴于N，由旋转的性质可证明△A′NP≌△PMA，得到A′N=PM=|m|，PN=AM=2，表示出A′坐标，将A′坐标代入抛物线解析式中求出相应m的值，即可确定出P的坐标．

试题解析：（1）∵抛物线（）与x轴交于点A（1，0）和点B（﹣3，0），∴OB=3，∵OC=OB，∴OC=3，∴c=3，∴，解得：，∴所求抛物线解析式为：；

（2）如图2，过点E作EF⊥x轴于点F，设E（a，）（﹣3＜a＜0），∴EF=，BF=a+3，OF=﹣a，∴S四边形BOCE==BFEF+（OC+EF）OF===，∴当a=时，S四边形BOCE最大，且最大值为．此时，点E坐标为（，）；

（3）∵抛物线的对称轴为x=﹣1，点P在抛物线的对称轴上，∴设P（﹣1，m），∵线段PA绕点P逆时针旋转90°后，点A的对应点A′恰好也落在此抛物线上，如图，∴PA=PA′，∠APA′=90°，如图3，过A′作A′N⊥对称轴于N，设对称轴于x轴交于点M，∴∠NPA′+∠MPA=∠NA′P+∠NPA′=90°，∴∠NA′P=∠NPA，在△A′NP与△APM中，∵∠A′NP=∠AMP=90°，∠NA′P=∠MPA，PA′=AP，∴△A′NP≌△PMA，∴A′N=PM=|m|，PN=AM=2，∴A′（m﹣1，m+2），代入得：，解得：m=1，m=﹣2，∴P（﹣1，1），（﹣1，﹣2）．