
 ШчЭМЃЌдкRtЁїABP1жаЃЌЁЯAP1B=RtЁЯЃЌЁЯA=30ЁуЃЌBP1=2ЃЌЙ§ЕуP1зїP1Q1ЁЭABЃЌДЙзуQ1ЃЌЙ§ЕуQ1зїQ1P2ЁЭAP1ЃЌДЙзуP2ЃЌЙ§ЕуP2зїP2Q2ЁЭABЃЌДЙзуQ2ЃЌЁШчДЫЮоЯоЯТШЅЃЌЕУЕНвЛЯЕСавѕгАШ§НЧаЮЁїP1Q1P2ЁЂЁїP2Q2P3ЁЂЁїP3Q3P4ЁЃЌдђЫљгаетаЉвѕгАШ§НЧаЮЕФУцЛ§КЭЪЧЃЈЁЁЁЁЃЉ
ШчЭМЃЌдкRtЁїABP1жаЃЌЁЯAP1B=RtЁЯЃЌЁЯA=30ЁуЃЌBP1=2ЃЌЙ§ЕуP1зїP1Q1ЁЭABЃЌДЙзуQ1ЃЌЙ§ЕуQ1зїQ1P2ЁЭAP1ЃЌДЙзуP2ЃЌЙ§ЕуP2зїP2Q2ЁЭABЃЌДЙзуQ2ЃЌЁШчДЫЮоЯоЯТШЅЃЌЕУЕНвЛЯЕСавѕгАШ§НЧаЮЁїP1Q1P2ЁЂЁїP2Q2P3ЁЂЁїP3Q3P4ЁЃЌдђЫљгаетаЉвѕгАШ§НЧаЮЕФУцЛ§КЭЪЧЃЈЁЁЁЁЃЉ| AЃЎ | $\sqrt{3}$ | BЃЎ | $\frac{3}{4}\sqrt{3}$ | CЃЎ | $\frac{6}{7}\sqrt{3}$ | DЃЎ | ВЛФмШЗЖЈ |
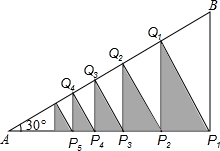
ЗжЮі ЯШИљОнШёНЧШ§НЧКЏЪ§ЕФЖЈвхЧѓГіAP1ЃЌBQ1ЃЌQ1P1МАQ1P2ЕФГЄЃЌдйЧѓГі$\frac{{S}_{{ЁїO}_{1}{P}_{1}{P}_{2}}}{{S}_{{ЁїBP}_{1}{Q}_{1}}}$ЕФжЕЃЌевГіЙцТЩМДПЩЕУГіНсТлЃЎ
НтД№ НтЃКЁпдкRtЁїABP1жаЃЌЁЯAP1B=RtЁЯЃЌЁЯA=30ЁуЃЌBP1=2ЃЌ
ЁрAP1=$\frac{{BP}_{1}}{tan30Ёу}$=$\frac{2}{\frac{\sqrt{3}}{3}}$=2$\sqrt{3}$ЃЌЁЯB=60ЁуЃЎ
ЁпP1Q1ЁЭABЃЌ
ЁрBQ1=BP1•cos60Ёу=2ЁС$\frac{1}{2}$=1ЃЌQ1P1=$\sqrt{3}$ЃЎ
ЁпQ1P2ЁЭAP1ЃЌ
ЁрQ1P2=P1Q1•sin60Ёу=$\sqrt{3}$ЁС$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$ЃЌQ1P2ЁЮBP1ЃЌ
Ёр$\frac{{S}_{{ЁїO}_{1}{P}_{1}{P}_{2}}}{{S}_{{ЁїBP}_{1}{Q}_{1}}}$=$\frac{{Q}_{1}{P}_{2}}{{BP}_{1}}$=$\frac{\frac{3}{2}}{2}$=$\frac{3}{4}$ЃЌ
ЁпSЁїBP1Q1=$\frac{1}{2}$ЁС1ЁС$\sqrt{3}$=$\frac{\sqrt{3}}{2}$ЃЌ
ЁрSЁїQ1P1P2=$\frac{3\sqrt{3}}{8}$ЃЌ
Ёр$\frac{{S}_{{ЁїO}_{1}{P}_{1}{P}_{2}}}{{S}_{ЫФБпаЮBP1P2Q1}}$=$\frac{\frac{3\sqrt{3}}{8}}{\frac{\sqrt{3}}{2}+\frac{3\sqrt{3}}{8}}$=$\frac{3}{7}$ЃЎ
ЭЌРэПЩЕУЃЌ$\frac{{S}_{{ЁїO}_{2}{P}_{2}{P}_{3}}}{{S}_{ЫФБпаЮO2Q1P2P3}}$=$\frac{3}{7}$ЃЌЁЃЌ
ЁрSвѕгА=$\frac{3}{7}$SЁїABP1=$\frac{3}{7}$ЁС$\frac{1}{2}$ЁС2$\sqrt{3}$ЁС2=$\frac{6\sqrt{3}}{7}$ЃЎ
ЙЪбЁCЃЎ
ЕуЦР БОЬтПМВщЕФЪЧЯрЫЦШ§НЧаЮЕФХаЖЈгыаджЪЃЌЪьжЊИпЯрЕШЕФШ§НЧаЮУцЛ§ЕФБШЕШгкЕзБпЕФБШЪЧНтД№ДЫЬтЕФЙиМќЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
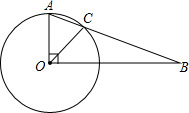 ШчЭМЃЌдкЁбOжаЃЌАыОЖOAЁЭOBЃЌЁЯB=28ЁуЃЌЧѓЁЯBOCЕФЖШЪ§ЃЎ
ШчЭМЃЌдкЁбOжаЃЌАыОЖOAЁЭOBЃЌЁЯB=28ЁуЃЌЧѓЁЯBOCЕФЖШЪ§ЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКНтД№Ьт
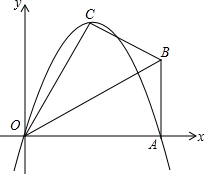 вбжЊЃЌдкRtЁїOABжаЃЌЁЯOAB=90ЁуЃЌЁЯBOA=30ЁуЃЌAB=2ЃЎШєвдOЮЊзјБъдЕуЃЌOAЫљдкжБЯпЮЊxжсЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЕуBдкЕквЛЯѓЯоФкЃЎНЋRtЁїOABбиOBелЕўКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуCДІЃЎ
вбжЊЃЌдкRtЁїOABжаЃЌЁЯOAB=90ЁуЃЌЁЯBOA=30ЁуЃЌAB=2ЃЎШєвдOЮЊзјБъдЕуЃЌOAЫљдкжБЯпЮЊxжсЃЌНЈСЂШчЭМЫљЪОЕФЦНУцжБНЧзјБъЯЕЃЌЕуBдкЕквЛЯѓЯоФкЃЎНЋRtЁїOABбиOBелЕўКѓЃЌЕуAТфдкЕквЛЯѓЯоФкЕФЕуCДІЃЎВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКбЁдёЬт
| AЃЎ | y=kx+b | BЃЎ | y=kx | CЃЎ | y=kx+bЃЈkЁй0ЃЉ | DЃЎ | y=x |
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃКЬюПеЬт
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com