
【题目】已知A(m,n),且满足m-2+(n-2)2=0,过A作AB⊥y轴,垂足为B.
(1)求A点坐标;
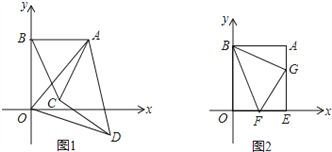
(2)如图1,分别以AB,AO为边作等边△ABC和△AOD,试判定线段AC和DC的数量关系和位置关系,并说明理由;
(3)如图2,过A作AE⊥x轴,垂足为E,点F、G分别为线段OE、AE上的两个动点 (不与端点重合),满足∠FBG=45°,设OF=a,AG=b,FG=c,试探究![]() 的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.
的值是 否为定值?如果是,直接写出此定值:如果不是,请举例说明.
【答案】(1)A(2,2);(2)AC=CD,AC⊥CD,理由见解析;(3)定值为0,
【解析】试题分析:(1)根据非负数的性质可得m、n的值;
(2)连接OC,由AB=BO知∠BAO=∠BOA=45°,由△ABC,△OAD为等边三角形知∠BAC=∠OAD=∠AOD=60°、OA=OD,继而由∠BAC-∠OAC=∠OAD-∠OAC得∠DAC=∠BAO=45°,根据OB=CB=2、∠OBC=30°知∠BOC=75°,∠AOC=∠BAO-∠BOA=30°,∠DOC=∠AOC=30°,证△OAC≌△ODC得AC=CD,再根据∠CAD=∠CDA=45°知∠ACD=90°,从而得AC⊥CD;
(3)在x轴负半轴取点M,使得OM=AG=b,连接BG,先证△BAG≌△BOM得∠OBM=∠ABG、BM=BG,结合∠FBG=45°知∠ABG+∠OBF=45°,从而得∠OBM+∠OBF=45°,∠MBF=∠GBF,再证△MBF≌△GBF得MF=FG,即a+b=c,代入原式可得答案.
试题解析:(1)由题得m=2,n=2,
∴A(2,2);
(2)如图1,连结OC,
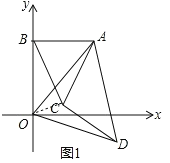
由(1)得AB=BO=2,
∴△ABO为等腰直角三角形,
∴∠BAO=∠BOA=45°,
∵△ABC,△OAD为等边三角形,
∴∠BAC=∠OAD=∠AOD=60°,OA=OD
∴∠BAC-∠OAC=∠OAD-∠OAC
即∠DAC=∠BAO=45°
在△OBC中,OB=CB=2,∠OBC=30°,
∴∠BOC=75°,
∴∠AOC=∠BAO-∠BOA=30°,
∴∠DOC=∠AOC=30°,
在△OAC和△ODC中,
∵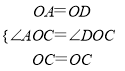 ,
,
∴△OAC≌△ODC,
∴AC=CD,
∴∠CAD=∠CDA=45°,
∴∠ACD=90°,
∴AC⊥CD;
(3)如图,在x轴负半轴取点M,使得OM=AG=b,连接BG,

在△BAG和△BOM中,
∵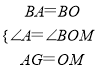 ,
,
∴△BAG≌△BOM
∴∠OBM=∠ABG,BM=BG
又∠FBG=45°
∴∠ABG+∠OBF=45°
∴∠OBM+∠OBF=45°
∴∠MBF=∠GBF
在△MBF和△GBF中,
∵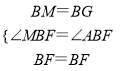 ,
,
∴△MBF≌△GBF
∴MF=FG
∴a+b=c代入原式=0.


科目:初中数学 来源: 题型:
【题目】下列命题是真命题的是( )
A.内错角相等
B.平面内,过一点有且只有一条直线与已知直线垂直
C.相等的角是对顶角
D.过一点有且只有一条直线与已知直线平行
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中国古代数学家们对于勾股定理的发现和证明,在世界数学史上具有独特的贡献和地位,体现了数学研究中的继承和发展.现用4个全等的直角三角形拼成如图所示“弦图”.Rt△ABC中,∠ACB=90°,若![]() ,请你利用这个图形解决下列问题:
,请你利用这个图形解决下列问题:
(1)试说明![]() ;
;
(2)如果大正方形的面积是10,小正方形的面积是2,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地生产一种绿色蔬菜,若在市场上直接销售,每吨利润为1 000元;经粗加工后销售,每吨利润可达4 500元;经精加工后销售,每吨利润涨至7 500元.
当地一家蔬菜公司收获这种蔬菜140吨,该公司加工厂的生产能力是:如果对蔬菜进行粗加工,每天可加工16吨;如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节等条件限制,公司必须在15天内将这批蔬菜全部销售或加工完毕,为此公司制订了三种方案:
方案一:将蔬菜全部进行粗加工;
方案二:尽可能多的对蔬菜进行精加工,没有来得及进行加工的蔬菜,在市场上直接销售;
方案三:将部分蔬菜进行精加工,其余蔬菜进行粗加工,并恰好15天完成.
你认为选择哪种方案获利最多?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口的直径 EF 长为10cm,母线OE(OF)长为10cm,在母线OF 上的点A 处有一块爆米花残渣且FA=2cm,一只蚂蚁从杯口的点E 处沿圆锥表面爬行到A 点,则此蚂蚁爬行的最短距离为 cm.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(﹣1,0),C(1,4),点B在x轴上,且AB=4.
(1)求点B的坐标,并画出△ABC;
(2)求△ABC的面积;
(3)在y轴上是否存在点P,使以A.B、P三点为顶点的三角形的面积为12?若存在,请直接写出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校初二年级在元旦汇演中需要外出租用同一种服装若干件,已知在没有任何优惠的情况下,甲服装店租用2件和在乙服装店租用3件共需280元,在甲服装店租用4件和在乙服装店租用一件共需260元.
(1)求两个服装店提供的单价分别是多少?
(2)若该种服装提前一周订货则甲乙两个租售店都可以给予优惠,具体办法如下:甲服装店按原价的八折进行优惠;在乙服装店如果租用5件以上,且超出5件的部分可按原价的六折进行优惠;设需要租用x件服装,选择甲店则需要y1元,选择乙店则需要y2元,请分别求出y1,y2关于x的函数关系式;
(3)若租用的服装在5件以上,请问租用多少件时甲乙两店的租金相同?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节期间,某食品店平均每天可卖出300只粽子,卖出1只粽子的利润是1元.经调查发现,零售单价每降0.1元,每天可多卖出100只粽子.为了使每天获取的利润更多,该店决定把零售单价下降m(0<m<1)元.
(1)零售单价下降m元后,该店平均每天可卖出___只粽子,利润为___元;
(2)在不考虑其他因素的条件下,当m定为多少时,才能使该店每天获取的利润是420元,并且卖出的粽子更多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两个同学分解因式x2+ax+b时,甲看错了b,分解结果为(x+2)(x+4),乙看错了a,分解结果为(x+1)(x+9),则2a+b=_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com