
����Ŀ������С�����½�50��ͣ��λ���Խ��С��ͣ���ѵ�����.��֪�½�1������ͣ��λ��1������ͣ��λ��0.5��Ԫ���½�3������ͣ��λ��2������ͣ��λ��1.1��Ԫ.
��1����С���½�1������ͣ��λ��1������ͣ��λ���������Ԫ��
��2������С��Ԥ��Ͷ�ʽ���10��Ԫ��������11��Ԫ�����м��ֽ��췽����
��3����֪ÿ������ͣ��λ�����100Ԫ��ÿ������ͣ��λ�����300Ԫ. �ڣ�2���������£��½�ͣ��λȫ�����.����С������һ������������е�3600Ԫ���ھɳ�λ��ά�ޣ�������������˽��³�λ��ǡ�����꣬��ֱ��д����С��ѡ��������ֽ��췽����
���𰸡���1���½�һ������ͣ��λ��0.1��Ԫ���½�һ������ͣ��λ��0.4��Ԫ����2����4�ֽ��췽������3�����췽���ǽ���32������ͣ��λ��18������ͣ��λ��
��������
��1�����½�һ������ͣ��λ��x��Ԫ���½�һ������ͣ��λ��y��Ԫ��������ã�![]() ����2�����½�m������ͣ��λ����10��0.1m+0.4��50��m����11���������⣻��3�����ݣ�2����������������з���.
����2�����½�m������ͣ��λ����10��0.1m+0.4��50��m����11���������⣻��3�����ݣ�2����������������з���.
�⣺��1�����½�һ������ͣ��λ��x��Ԫ���½�һ������ͣ��λ��y��Ԫ��������ã�
![]() ��
��
���![]() ��
��
���½�һ������ͣ��λ��0.1��Ԫ���½�һ������ͣ��λ��0.4��Ԫ��
��2�����½�m������ͣ��λ����
10��0.1m+0.4��50��m����11��
���30��m��![]() ��
��
��ΪmΪ����������m��30��m��31��m��32��m��33��
��Ӧ��50��m��20��50��m��19��50��m��18��50��m��17��
����4�ֽ��췽����
��3��������ͣ��λ��30ʱ�����£�20��30��100+20��300��9000���õ�3600��ʣ��9000��3600��5400����Ϊ��һ������ͣ��λ�ķ�����1000��һ��������4000.5400���ܴճ����������Բ��������⣮
ͬ���ã�������ͣ��λ��31��33ʱ�������ܴճ�������
���㵽����ͣ��λ��32ʱ������ͣ��λ��18��
��32��100+18��300��8600��8600��3600��5000��
��ʱ�ɴճ���1������ͣ������һ������ͣ��λ��1000+4000��5000��
���Դ���32��18��
�𣺽��췽���ǽ���32������ͣ��λ��18������ͣ��λ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
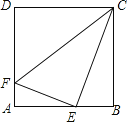
����Ŀ����֪������ABCD�ı߳�Ϊ4��EΪAB���е㣬FΪAD��һ�㣬��AF=![]() AD�����жϡ�EFC����״��
AD�����жϡ�EFC����״��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������P��ƽ��ֱ������ϵ�а�ͼ�м�ͷ��ʾ�����˶�����1�δ�ԭ���˶����㣨1��1������2�ν����˶����㣨2��0������3�ν����˶����㣨3��2�������������������˶����ɣ�������2019���˶�����P�������ǣ�������

A. ��2018��1��B. ��2018,0��C. ��2019,2�� D. ��2019,1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�˽�ѧ������ѵ���������ij�д�ȫ�о��꼶ѧ���������ȡ����ѧ��������һ��������Ŀ���ԣ��Ѳ��Խ����Ϊ�ĸ��ȼ���A����B����C����D�����������Ǹ����Խ�����������������������ͳ��ͼ�������ͳ��ͼ�е���Ϣ����������⣺

��1�����γ������Ե�ѧ���������� ����
��2������ͼ�С����Ķ������� ������������ͳ��ͼ����������
��3����A��B��C��D�ĸ��ȼ����θ���Ϊ90��75��65��55����λ���֣������磺�ȼ�ΪA��ͬѧ�����÷�Ϊ90�֣������������ƣ����о��꼶����ѧ��32000�������ȫ���μ�����������ԣ����Ƹ��о��꼶������60�����£�ѧ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��˾����![]() �����豸����֪ÿ̨
�����豸����֪ÿ̨![]() ���豸�ijɱ���
���豸�ijɱ���![]() ���豸��1��5������˾��Ͷ��6��Ԫ����
���豸��1��5������˾��Ͷ��6��Ԫ����![]() ���豸��Ͷ��15��Ԫ����
���豸��Ͷ��15��Ԫ����![]() ���豸��������������豸��40̨�������������⣺
���豸��������������豸��40̨�������������⣺
��1��![]() �����豸ÿ̨�ijɱ��ֱ��Ƕ�����Ԫ��
�����豸ÿ̨�ijɱ��ֱ��Ƕ�����Ԫ��
��2����![]() �����豸ÿ̨���ۼ۷ֱ���5000Ԫ��9000Ԫ����˾�������������豸��50̨��������
�����豸ÿ̨���ۼ۷ֱ���5000Ԫ��9000Ԫ����˾�������������豸��50̨��������![]() ���豸��������10̨���ƻ����ۺ����������12��Ԫ�����ʲ�����������������˾���������������������
���豸��������10̨���ƻ����ۺ����������12��Ԫ�����ʲ�����������������˾���������������������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1�����κ���y1=(x��2)(x��4)��ͼ����x�ύ��A��B���㣨��A�ڵ�B����ࣩ����Գ���l��x�ύ�ڵ�C�����Ķ���Ϊ��D��
��1�����D������ ��
��2����P�ڶԳ���l�ϣ�λ�ڵ�C�Ϸ�����CP=2CD����PΪ����Ķ��κ���y2=ax2+bx+c��a��0����ͼ�����A��
����˵�����κ���y2=ax2+bx+c��a��0����ͼ�����B��
�ڵ�R�ڶ��κ���y1=��x��2����x��4����ͼ���ϣ���x��ľ���Ϊd������R������Ϊ ʱ�����κ���y2=ax2+bx+c��a��0����ͼ��������ֻ�������㵽x��ľ������2d��
����ͼ2����֪0��m��2������M��0��m����x���ƽ���ߣ��ֱ��κ���y1=��x��2����x��4��y2=ax2+bx+c��a��0����ͼ���ڵ�E��F��G��H����E��G�ڶԳ���l��ࣩ������H��x��Ĵ��ߣ�����Ϊ��N�������κ���y1=��x��2����x��4����ͼ���ڵ�Q������GHN�ס�EHQ����ʵ��m��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ij����������У���Ա�״����ŵײ����ĵ�O����ǰ��10m��������ţ������������߷������������ߣ�������������߶�Ϊ3mʱ�ﵽ��ߵ㣬��ʱ������е�ˮƽ����Ϊ6m����֪���ŵĺ�����Ϊ2.44m��
��1������ͼ��ʾ��ƽ��ֱ������ϵ�У��ʴ˷��������ܷ�����ţ����������������
��2������Ա��վ�ھ�������2m����������ʱ�ֵ��������Ϊ2.52m��������ֹ��Ա�Ĵ˴�������������ܣ������ٺ��˶�Զ������ֹ��Ա�����ţ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y1=a��x+2��2��3��y2=![]() ��x��3��2+1���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C�������½��ۣ�
��x��3��2+1���ڵ�A��1��3��������A��x���ƽ���ߣ��ֱ������������ڵ�B��C�������½��ۣ�
������xȡ��ֵ��y2��ֵ����������
��a=1��
�۵�x=0ʱ��y2��y1=4��
��2AB=3AC��
������ȷ�����ǣ�������

A. �٢� B. �ڢ� C. �ۢ� D. �٢�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������Ŀڴ���װ�к졢�ơ���������ɫ��С�����ɸ�������ɫ�������ͬ�������к���2�����ֱ����1�š�2�ţ�������1������������������һ������������ĸ���Ϊ![]() ��
��
��1������л���ĸ�����
��2����һ����������һ�����Żأ����ڶ���������һ�������û���״ͼ���б���ķ�����������������ͬ��ɫ��ĸ��ʣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com