
 ��֪����ͼ���ı���ABCD�У�AD��BC������AC��BD���ڵ�O�����AOD����AOB����BOC����COD������ֱ�ΪS1��S2��S3��S4��
��֪����ͼ���ı���ABCD�У�AD��BC������AC��BD���ڵ�O�����AOD����AOB����BOC����COD������ֱ�ΪS1��S2��S3��S4������ ��1����A��D�ֱ���AE��BC��E��DF��BC��F������ͬ�ȸߵ����������������ȵõ�S��ABC=S��DBC��֤�����ۣ�
��2������������S1�ֱ��ʾS2��S3���������ͷǸ��������ʽ����жϼ��ɣ�
��� ֤������1����A��D�ֱ���AE��BC��E��DF��BC��F��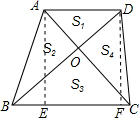
��AD��BC��
��AE=DF��
��S��ABC=S��DBC��
��S��ABC-S��OBC=S��DBC-S��OBC����S��ABO=S��DCO��
��S2=S4��
��2����$\frac{{S}_{1}}{{S}_{2}}=\frac{m}{n}$��
��S2=$\frac{n}{m}$S1��
��$\frac{{S}_{1}}{{S}_{3}}$=$\frac{{m}^{2}}{{n}^{2}}$��
��S3=$\frac{{n}^{2}}{{m}^{2}}$S1��
��S3+S1=$\frac{{n}^{2}+{m}^{2}}{{m}^{2}}$S1��
��S2=S4��
��S2+S4=$\frac{2n}{m}$S1��
�ࣨS1+S3��-��S2+S4��=$\frac{{n}^{2}+{m}^{2}}{{m}^{2}}$S1-$\frac{2n}{m}$S1=$\frac{��m-n��^{2}}{{m}^{2}}$S1��
��m=nʱ��$\frac{��m-n��^{2}}{{m}^{2}}$=0��
S1+S3=S2+S4��
��m��nʱ��$\frac{��m-n��^{2}}{{m}^{2}}$��0��
��S1+S3��-��S2+S4����0��
��S1+S3������S2+S4����
���� ���⿼�����������Ȼ��任�����յȵȸߵ����������������ȡ����������ε�����ȵ������Ʊȵ�ƽ���Լ����������ǽ���Ĺؼ���


 ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
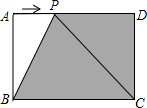 ��ͼ���ڳ�����ABCD�У�AB=4cm��BC=5cm����P�ӵ�A��ʼ��1cm/s���ٶ����D�˶������P�˶���ʱ��Ϊt��s������Ӱ���ֵ����ΪS��cm2����
��ͼ���ڳ�����ABCD�У�AB=4cm��BC=5cm����P�ӵ�A��ʼ��1cm/s���ٶ����D�˶������P�˶���ʱ��Ϊt��s������Ӱ���ֵ����ΪS��cm2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���� | B�� | ������ | C�� | ������ | D�� | Բ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com