
【题目】如图,两个同心圆的半径分别为4cm和5cm,大圆的一条弦AB与小圆相切,则弦AB的长为( ) 
A.6cm
B.4cm
C.3cm
D.8cm
【答案】A
【解析】解:如图,连接OC,AO, 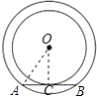
∵大圆的一条弦AB与小圆相切,
∴OC⊥AB,
∴AC=BC= ![]() AB,
AB,
∵OA=5cm,OC=4cm,
在Rt△AOC中,AC= ![]() =3cm,
=3cm,
∴AB=2AC=6(cm).
故选A.
【考点精析】掌握切线的性质定理和圆与圆的位置关系是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;两圆之间有五种位置关系:无公共点的,一圆在另一圆之外叫外离,在之内叫内含;有唯一公共点的,一圆在另一圆之外叫外切,在之内叫内切;有两个公共点的叫相交.两圆圆心之间的距离叫做圆心距.两圆的半径分别为R和r,且R≥r,圆心距为P:外离P>R+r;外切P=R+r;相交R-r<P<R+r;内切P=R-r;内含P<R-r.


科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的直径AB与弦CD相交于点E,AB⊥CD,⊙O的切线BF与弦AD的延长线相交于点F.若⊙O的半径为5,cos∠BCD= ![]() ,那么线段AD= .
,那么线段AD= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正△ABC内接于⊙O,P是劣弧BC上任意一点,PA与BC交于点E,有如下结论:①PA=PB+PC;② ![]() ;③PAPE=PBPC.其中,正确结论的个数为( )
;③PAPE=PBPC.其中,正确结论的个数为( ) 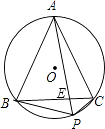
A.3个
B.2个
C.1个
D.0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了减轻学生课业负担,提高课堂效果,我县教体局积极推进 “高效课堂”建设.
某学校的《课堂检测》印刷任务原来由甲复印店承接,其每月收费y(元)与复印页数x(页)的函数关系如图所示:
⑴从图象中可看出:每月复印超过500页部分每页收费 元;
⑵现在乙复印店表示:若学校先按每月付给200元的月承包费,则可按每页0.15元收费.乙复印店每月收费y(元)与复印页数x(页)的函数关系为 ;
⑶在给出的坐标系内画出(2)中的函数图象,并结合函数图象回答每月复印在3000页左右应选择哪个复印店?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,对角线AD,BC交于点O,点E、F分别在AC,CD边上,EF∥AD,交BC于点P,若点O是△BEF的重心.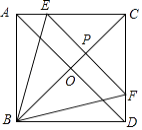
(1)求tan∠ABE的值.
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿东北方向向海岛B航行,其速度为15海里/小时;乙船速度为20海里/小时,先沿正东方向航行1小时后,到达C港口接旅客,停留半小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
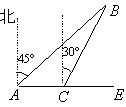
(1)求港口A到海岛B的距离;
(2)B岛建有一座灯塔,在离灯塔方圆5海里内都可以看见灯塔,问甲、乙两船哪一艘先看到灯塔?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】五一期间刚到深圳的小明在哥哥的陪伴下,打算上午从莲山春早、侨城锦绣、深南溢彩中随机选择一个景点,下午从梧桐烟云、梅沙踏浪、一街两制中随机选择一个景点,小明恰好上午选中莲山春早,下午选中梅沙踏浪的概率是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,将一块腰长为 ![]() 的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.
的等腰直角三角板ABC放在第二象限,且斜靠在两坐标轴上,直角顶点C的坐标为(﹣1,0),点B在抛物线y=ax2+ax﹣2上.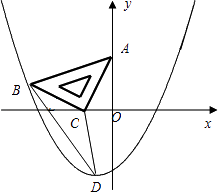
(1)点A的坐标为 , 点B的坐标为;
(2)抛物线的解析式为;
(3)设(2)中抛物线的顶点为D,求△DBC的面积;
(4)在抛物线上是否还存在点P(点B除外),使△ACP仍然是以AC为直角边的等腰直角三角形?若存在,请直接写出所有点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com