
【题目】我们把a、b两个数中较小的数记作min{a,b},直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,则k的取值为 .
【答案】2﹣2![]() 或
或![]() 或﹣1.
或﹣1.
【解析】
试题分析:根据题意,x2﹣1<﹣x+1,即x2+x﹣2<0,
解得:﹣2<x<1,
故当﹣2<x<1时,y=x2﹣1;
当x≤﹣2或x≥1时,y=﹣x+1;
函数图象如下:
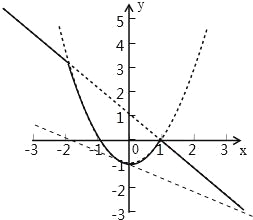
由图象可知,∵直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,且k<0,
①直线y=kx﹣k﹣2经过点(﹣2,3)时,3=﹣2k﹣k﹣2,k=![]() ,此时直线y=
,此时直线y=![]() x
x![]() ,与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
,与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
②直线y=kx﹣k﹣2与函数y=x2﹣1相切时,由 消去y得x2﹣kx+k+1=0,∵△=0,k<0,
消去y得x2﹣kx+k+1=0,∵△=0,k<0,
∴k2﹣4k﹣4=0,
∴k=2﹣2![]() (或2+2
(或2+2![]() 舍弃),此时直线y=(2﹣2
舍弃),此时直线y=(2﹣2![]() )x﹣4+2
)x﹣4+2![]() 与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
③直线y=kx﹣k﹣2和直线y=﹣x+1平行,k=﹣1,直线为y=﹣x﹣1与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点.
综上,k=2﹣2![]() 或-
或-![]() 或﹣1.
或﹣1.
故答案为:2﹣2![]() 或-
或-![]() 或﹣1.
或﹣1.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知在RtABC中,∠C=90°,∠A=30°,在直线AC上找点P,使△ABP是等腰三角形,则∠APB的度数为_______________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是( )
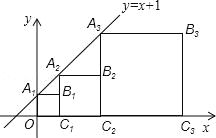
A.(63,32) B.(64,32) C.(63,31) D.(64,31)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在高速公路上,从3千米处开始,每隔4千米设置一个限速标志牌,而且从10千米处开始,每隔9千米设置一个速度监控仪,刚好在19千米处同时经过这两种标志.则第三次同时经过这两种标志的地点的千米数为( )
A.32B.55C.91D.127
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上A,B两点对应的有理数分别为10和15,点P从点A出发,以每秒1个单位长度的速度沿数轴正方向运动,点Q同时从原点O出发,以每秒2个单位长度的速度沿数轴正方向运动,设运动时间为t秒.
(1)当0<t<5时,用含t的式子表示BP,AQ
(2)当t=2时,求PQ的值;
(3)当PQ=![]() AB时,求t的值.
AB时,求t的值.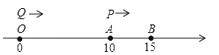
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列各式中能够成立的是( )
A. (x+2y)2=x2+2xy+4y2 B. (x+2y)2=x2+4y2
C. (x﹣y)2=x2﹣2xy﹣y2 D. (a﹣b)2=(b﹣a)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读,然后解答提出的问题:
设a,b是有理数,且满足a+![]() b=3﹣2
b=3﹣2![]() ,求ba的值.
,求ba的值.
解:由题意得(a﹣3)+(b+2)![]() =0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
=0,因为a,b都是有理数,所以a﹣3,b+2也是有理数,
由于![]() 是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+
是无理数,所以a﹣3=0,b+2=0,所以a=3,b=﹣2,所以ba=(﹣2)3=﹣8.问题:设x,y都是有理数,且满足x2﹣2y+![]() y=8+4
y=8+4![]() ,求x+y的值.
,求x+y的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com