
已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.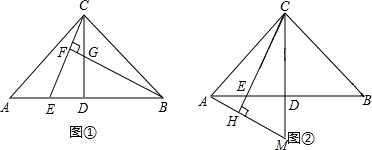
(1)直线BF垂直于CE于点F,交CD于点G(如图1),求证:AE=CG;
(2)直线AH垂直于CE,垂足为H,交CD的延长线于点M(如图2),求证:△BCE≌△CAM.
【考点】全等三角形的判定与性质;等腰直角三角形.
【分析】(1)先证出∠ACE=∠CBG,再由ASA证明△ACE≌△CBG,得出对应边相等即可;
(2)先证出∠CEB=∠CMA,再由AAS证明△BCE≌△ACM.
【解答】解:(1)∵点D是AB的中点,AC=BC,∠ACB=90°,
∴CD⊥AB,∠ACD=∠BCD=45°,∠CAD=∠CBD=45°.
∴∠CAE=∠BCG.
又BF⊥CE,
∴∠CBG+∠BCF=90°.
又∠ACE+∠BCF=90°,
∴∠ACE=∠CBG.
在△AEC和△CGB中,

∴△AEC≌△CGB.
∴AE=CG.
(2)∵CH⊥HM,CD⊥ED,
∴∠CMA+∠MCH=90°,∠BEC+∠MCH=90°.
∴∠CMA=∠BEC.
又AC=BC,∠ACM=∠CBE=45°,
在△BCE和△CAM中

∴∠BCE≌△CAM(AAS).
【点评】本题考查了全等三角形的判定与性质;熟练掌握全等三角形的判定方法是解决问题的关键.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:初中数学 来源: 题型:
下列说法错误的说法有几个 ( )
① 全等三角的对应边相等; ②全等三角形的对应角相等; ③全等三角形的面积相等; ④全等三角形的周长相等; ⑤有两边和第三边上的高对应相等的两个三角形全等; ⑥全等三角形的对应边上的中线相等;
② A、1个 B、2个 B、3个 D、5个
查看答案和解析>>
科目:初中数学 来源: 题型:
点A、B在数轴上的位置如图所示:
(1)点A表示的数是__________,点B表示的数是__________;
(2)在原图中分别标出表示+1.5的点C、表示﹣3.5的点D;
(3)在上述条件下,B、C两点间的距离是__________,A、C两点间的距离是__________.
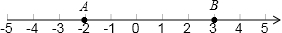
查看答案和解析>>
科目:初中数学 来源: 题型:
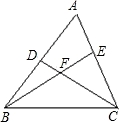
.已知:如图,D是AB上一点,E是AC上的一点,BE、CD相交于点F,∠A=62°,∠ACD=35°,∠ABE=20°.求:(1)∠BDC的度数; (2)∠BFD的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com