
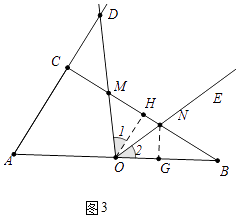
����Ŀ����ͼ����ֱ��������ABC�У���ACB=90�㣬AB=10��sinB= ![]() ����O��AB���е㣬��DOE=��A������DOE�Ե�OΪ��ת������תʱ��OD��AC���ӳ����ڵ�D������CB�ڵ�M��OE���߶�BM�ڵ�N��
����O��AB���е㣬��DOE=��A������DOE�Ե�OΪ��ת������תʱ��OD��AC���ӳ����ڵ�D������CB�ڵ�M��OE���߶�BM�ڵ�N��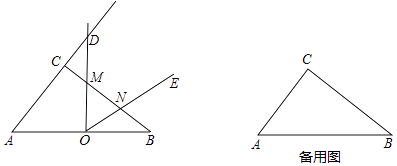
��1����CM=2ʱ�����߶�CD�ij���
��2����CM=x��BN=y������y��x֮��ĺ�������ʽ����д��������
��3�������OMN����OMΪ���ĵ��������Σ���ֱ��д���߶�CM�ij���
���𰸡�
��1��
�⣺��ͼ1�У���OH��BC��H��
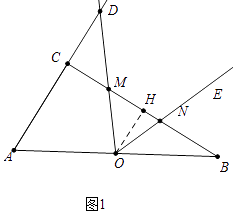
��Rt��ABC����AB=10��sinB= ![]() ��
��
��AC=6��BC=8��
��AO=OB��OH��AC��
��CH=HB=4��OH=3��
��CM=2��
��CM=HM=2��
�ڡ�DCM�͡�OHM�У�
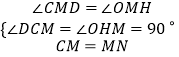 ��
��
���DCM�ա�OHM��
��CD=OH=3��
��2��
�⣺�⣺��ͼ2�У���NG��OB��G��
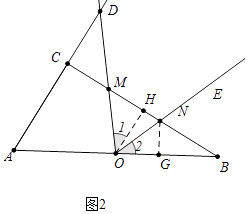
�ߡ�HOB=��A=��MON��
���1=��2��
��Rt��BNG��BN=y��sibB= ![]() ��
��
��GN= ![]() y��BG=
y��BG= ![]() y��
y��
��tan��1=tan��2��
�� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��y= ![]() ����0��x��4��
����0��x��4��
��3��
����ͼ3�У���OM=ONʱ��OH��ֱƽ��MN��
��BN=CM=x��
�ߡ�OMH�ա�ONG��
��NG=HM=4��x��
��sinB= ![]() ��
��
�� ![]() =
= ![]() ��
��
��CM=x= ![]() ��
��
����ͼ4�У���OM=MNʱ������CO��
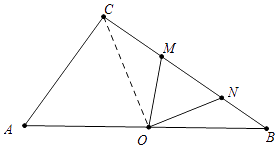
��OA=OB��OM=MN��
��CO=OA=OB��
���MON=��MNO=��A=��OCA��
���MON�ס�OAC��
���AOC=��OMN��
���BOC=��CMO���ߡ�B=��B��
���CMO�ס�COB��
�� ![]() =
= ![]() ��
��
��8x=52��
��x= ![]() ��
��
������������OMN����OMΪ���ĵ���������ʱ���߶�CM�ij�Ϊ ![]() ��
�� ![]()
����������1����ͼ1�У���OH��BC��H��ֻҪ֤����DCM�ա�OHM�����ɵó�CD=OH=3����2����ͼ2�У���NG��OB��G������֤����1=��2������tan��1=tan��2���ɵ� ![]() =
= ![]() ���ɴ˼��ɽ�����⣮��3���������������ۼ��ɢ���ͼ3�У���OM=ONʱ��OH��ֱƽ��MN������ͼ4�У���OM=MNʱ���ֱ���⼴�ɣ�
���ɴ˼��ɽ�����⣮��3���������������ۼ��ɢ���ͼ3�У���OM=ONʱ��OH��ֱƽ��MN������ͼ4�У���OM=MNʱ���ֱ���⼴�ɣ�


 �żӾ���ϵ�д�
�żӾ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+![]() x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0��������AB��AC��
x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0��������AB��AC��
��1����ֱ��д�����κ���y=ax2+![]() x+c�ı���ʽ��
x+c�ı���ʽ��
��2���жϡ�ABC����״����˵�����ɣ�
��3������N��x�����˶������Ե�A��N��CΪ������������ǵ���������ʱ����ֱ��д����ʱ��N�����ꣻ
��4������N���߶�BC���˶��������B��C�غϣ�������N��NM��AC����AB�ڵ�M������AMN������ʱ�����ʱ��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У�����C1�ķ���Ϊ ![]() ��������ԭ��Ϊ���㣬��x���������Ϊ���ᣬ����������ϵ������C2�ļ����귽��Ϊ��2��8��sin��+15=0�� ����д��C1�IJ������̺�C2��ֱ�����귽�̣�
��������ԭ��Ϊ���㣬��x���������Ϊ���ᣬ����������ϵ������C2�ļ����귽��Ϊ��2��8��sin��+15=0�� ����д��C1�IJ������̺�C2��ֱ�����귽�̣�
�������P��C1�ϣ���Q��C2�ϣ���|PQ|�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ı���ABCD�Ǿ��Σ�cot��ADB= ![]() ��AB=16����E������BC�ϣ���F���߶�BD�ϣ��ҡ�DEF=��ADB��
��AB=16����E������BC�ϣ���F���߶�BD�ϣ��ҡ�DEF=��ADB��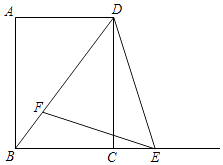
��1�����߶�BD�ij���
��2����BE=x����DEF�����Ϊy����y����x�ĺ�����ϵʽ����д������������
��3������DEFΪ����������ʱ�����߶�BE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����ı���ABCD�У�AB��CD���Խ���AC��BD���ڵ�E����F�ڱ�AB�ϣ�����CF���߶�BE�ڵ�G��CG2=GEGD�� 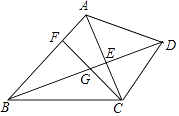
��1����֤����ACF=��ABD��
��2������EF����֤��EFCG=EGCB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD�ǡ�O��ֱ����BC�ǡ�O���ң�AD��BC������Ϊ��E��AE=BC=16�����O��ֱ���� 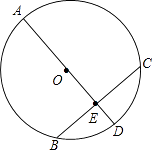
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
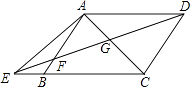
����Ŀ����ͼ����֪���ı���ABCD�У�AD��BC��EΪ��CB�ӳ�����һ�㣬����DE����AB�ڵ�F������AC��DE�ڵ�G���� ![]() =
= ![]() ��
�� 
��1����֤��AB��CD��
��2�����AD2=DGDE����֤�� ![]() =
= ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�MΪCD�е㣬�ֱ���B��MΪԲ�ģ���BC����MC��Ϊ�뾶�����������ཻ�ڵ�P������PBC=70�㣬���MPC�Ķ���Ϊ�� �� 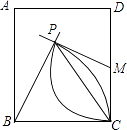
A.55��
B.40��
C.35��
D.20��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y= ![]() ��aΪ��������ͼ����B����4��2����
��aΪ��������ͼ����B����4��2����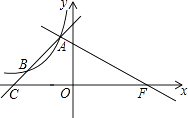
��1����a��ֵ��
��2����ͼ������B��ֱ��AB�뺯��y= ![]() ��ͼ���ڵ�A����x�ύ�ڵ�C����AB=3BC������A��ֱ��AF��AB����x���ڵ�F�����߶�AF�ij���
��ͼ���ڵ�A����x�ύ�ڵ�C����AB=3BC������A��ֱ��AF��AB����x���ڵ�F�����߶�AF�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com