
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD. 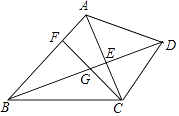
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
【答案】
(1)证明:∵CG2=GEGD,
∴ ![]() .
.
又∵∠CGD=∠EGC,
∴△GCD∽△GEC.
∴∠GDC=∠GCE.
∵AB∥CD,
∴∠ABD=∠BDC.
∴∠ACF=∠ABD.
(2)证明:∵∠ABD=∠ACF,∠BGF=∠CGE,
∴△BGF∽△CGE.
∴ ![]() .
.
又∵∠FGE=∠BGC,
∴△FGE∽△BGC.
∴ ![]() .
.
∴FECG=EGCB.
【解析】(1)先根据CG2=GEGD得出 ![]() ,再由∠CGD=∠EGC可知△GCD∽△GEC,∠GDC=∠GCE.根据AB∥CD得出∠ABD=∠BDC,故可得出结论;(2)先根据∠ABD=∠ACF,∠BGF=∠CGE得出△BGF∽△CGE,故
,再由∠CGD=∠EGC可知△GCD∽△GEC,∠GDC=∠GCE.根据AB∥CD得出∠ABD=∠BDC,故可得出结论;(2)先根据∠ABD=∠ACF,∠BGF=∠CGE得出△BGF∽△CGE,故 ![]() .再由∠FGE=∠BGC得出△FGE∽△BGC,进而可得出结论.
.再由∠FGE=∠BGC得出△FGE∽△BGC,进而可得出结论.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4个分别标有数字﹣1,﹣2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是___;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜;点P(x,y)在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,AB=9,cosB= ![]() ,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 .
,把△ABC绕着点C旋转,使点B与AB边上的点D重合,点A落在点E,则点A,E之间的距离为 . 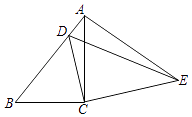
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=3,BC=2,边AB的垂直平分线交AC边于点D,交AB边于点E,联结DB,那么tan∠DBC的值是 . 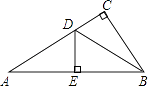
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角三角形ABC中,∠ACB=90°,AB=10,sinB= ![]() ,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.
,点O是AB的中点,∠DOE=∠A,当∠DOE以点O为旋转中心旋转时,OD交AC的延长线于点D,交边CB于点M,OE交线段BM于点N.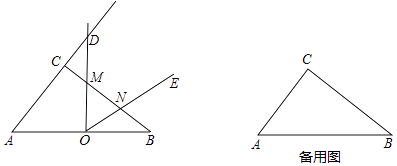
(1)当CM=2时,求线段CD的长;
(2)设CM=x,BN=y,试求y与x之间的函数解析式,并写出定义域;
(3)如果△OMN是以OM为腰的等腰三角形,请直接写出线段CM的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE= ![]() AD,过点A作AF∥BC,交EC的延长线于点F.
AD,过点A作AF∥BC,交EC的延长线于点F. 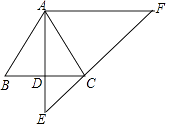
(1)设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,用
,用 ![]() 、
、 ![]() 的线性组合表示
的线性组合表示 ![]() ;
;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1 , 作第二个正方形A1B1C1C;延长C1B1交x轴于点A2 , 作第三个正方形A2B2C2C1 , …,按这样的规律进行下去,第2016个正方形的面积为( ) 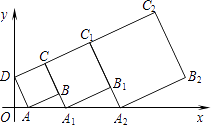
A.20×( ![]() )4030
)4030
B.20×( ![]() )4032
)4032
C.20×( ![]() )2016
)2016
D.20×( ![]() )2015
)2015
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com