
����Ŀ��һ�������Ŀڴ���װ��4���ֱ�������֩�1����2��3��4��С�����ǵ���״����С��ȫ��ͬ��С���ȴӿڴ����������һ��С���������Ϊx��Сӱ��ʣ�µ�3��С�����������һ��С���������Ϊy��
��1��С��������������3��С��ĸ�����___��
��2�������б�������״ͼ�ķ�����ʾ����x��yȷ���ĵ�P��x��y�����п��ܵĽ����
��3�����涨����P��x��y���ڵ�һ�����������С���ʤ����P��x��y���ڵڶ��������������Сӱ��ʤ����ֱ�������˻�ʤ�ĸ��ʣ�
���𰸡�
��1��
�⣺С��������������3��С��ĸ�����![]() ��
��
�ʴ�Ϊ![]() ��
��
��2��
�⣺�б����£�
��1 | ��2 | 3 | 4 | |
��1 | ����1����2�� | ����1��3�� | ����1��4�� | |
��2 | ����2����1�� | ����2��3�� | ����2��4�� | |
3 | ��3����1�� | ��3����2�� | ��3��4�� | |
4 | ��4����1�� | ��4����2�� | ��4��3�� |
��3��
�⣺������ı�����Կ��������п��ܳ��ֵĽ������12�֣���ÿ�ֽ�����ֵĿ�������ͬ�����е㣨x��y���ڵ�һ����������Ľ����4�֣��ڶ�����������Ľ����8�֣�
����С���ʤ�ĸ���=![]() ��Сӱ��ʤ�ĸ���=
��Сӱ��ʤ�ĸ���=![]() ��
��
����������1��ֱ�Ӹ��ݸ��ʹ�ʽ��⣻
��2��ͨ���б�չʾ����12�ֵȿ����ԵĽ������
��3���ҳ��ڵ�һ����������Ľ�����͵ڶ�����������Ľ������Ȼ����ݸ��ʹ�ʽ�������˻�ʤ�ĸ��ʣ�


 �����Ծ���ĩ���100��ϵ�д�
�����Ծ���ĩ���100��ϵ�д� ˫��ͬ������ѵ��ϵ�д�
˫��ͬ������ѵ��ϵ�д� �Ƹ�С״Ԫͬ������������ϵ�д�
�Ƹ�С״Ԫͬ������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����A��˫����![]() �ڵڶ�����֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ����������ABC���ҡ�ACB=120�㣬��C�ڵ�һ���ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����
�ڵڶ�����֧�ϵ�һ�����㣬����AO���ӳ�����һ��֧�ڵ�B����ABΪ����������ABC���ҡ�ACB=120�㣬��C�ڵ�һ���ޣ����ŵ�A���˶�����C��λ��Ҳ���ϱ仯������Cʼ����˫����![]() ���˶�����k��ֵΪ��������
���˶�����k��ֵΪ��������
A.1
B.2
C.3
D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧҪ����������ʵ����ԣ����þ��꼶�����༶��ѧ������ʵ�����ģ���֪һ���������Ҫ30������ɣ�
��1�����һ������ͬ����15���Ӻ�һ������������Ҫ�뿪��ʣ����ɶ��������15���Ӳ����������������������ʵ��������Ҫ���ٷ��ӣ�
��2�����һ�����Ĺ���Ч�ʲ��䣬���ɶ����������ʱ�䲻����20���ӣ�ʣ�������һ�������ɣ���ô��������������һ�����ٻ���Ҫ���ٷ��ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�������У�������ÿ��С�����εı߳���Ϊ1�����ν���λ�Ʊ任����ԳƱ任��ƽ�Ʊ任��õ���A3B3C3 �� 
��1����ABC���A1B1C1��λ�Ʊȵ���������
��2���������л�����A1B1C1����y�����Գ�ͼ�Ρ�A2B2C2��
��3����д����A3B3C3���ɡ�A2B2C2����ƽ�Ƶõ��ģ�
��4�����P��x��y��Ϊ��ABC��һ�㣬���ξ����������α任��P�Ķ�Ӧ�������Ϊ���� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ABCD�ĶԽ���AC���е�O��EF��AC����BC���ڵ�E����AD���ڵ�F���ֱ�����AE��CF����AB=![]() ����DCF=30�㣬��EF�ij�Ϊ��������
����DCF=30�㣬��EF�ij�Ϊ��������
A.2
B.3
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+![]() x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0��������AB��AC��
x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0��������AB��AC��
��1����ֱ��д�����κ���y=ax2+![]() x+c�ı���ʽ��
x+c�ı���ʽ��
��2���жϡ�ABC����״����˵�����ɣ�
��3������N��x�����˶������Ե�A��N��CΪ������������ǵ���������ʱ����ֱ��д����ʱ��N�����ꣻ
��4������N���߶�BC���˶��������B��C�غϣ�������N��NM��AC����AB�ڵ�M������AMN������ʱ�����ʱ��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���D��E��F�ֱ���AB��BC��AC�ϣ��ҡ�ADF+��DEC=180�㣬��AFE=��BDE��
��1����ͼ1����DE=DFʱ��ͼ1���Ƿ������AB��ȵ��߶Σ������ڣ����ҳ���������֤�����������ڣ�˵�����ɣ�
��2����ͼ2����DE=kDF������0��k��1��ʱ������A=90�㣬AF=m����BD�ij����ú�k��m��ʽ�ӱ�ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������ˮ�����������£�ԭʼ��ˮ���Ⱦ���Aϵͳ���������������ˮ��A��ˮ���ﵽ����������ƴ�꣩�ĸ���Ϊp��0��p��1�����������⣬��ȷ�ϴ����ֱ���ŷţ����������������Bϵͳ������ֱ���ŷţ� ij������4����ˮ����A��ˮ�أ��ֱ�ȡ������⣮�����ˮ�������ʱ���ȿ���������飬Ҳ���Խ����ɸ����������һ���飮���������ֻҪ����������꣬���������Ļ������ز���꣮�������������꣬������и�������������������飻�����������꣬��ԭˮ�ص���ˮֱ���ŷţ�
�����������ַ�����
����һ��������飻
��������ƽ���ֳ����黯�飻
��������������������һ���飬ʣ�µ�һ���������飻
�����ģ�����һ���飮
�������������ֵԽС������Խ���š���
���� �� ![]() ����2��A��ˮ������ϻ����������ĸ��ʣ�
����2��A��ˮ������ϻ����������ĸ��ʣ�
���� �� ![]() ������4��A��ˮ������Ҫ���飬���ʣ�����һ�����������ĸ���š���
������4��A��ˮ������Ҫ���飬���ʣ�����һ�����������ĸ���š���
���� �������������ȡ������ġ������š�����p��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����ı���ABCD�У�AB��CD���Խ���AC��BD���ڵ�E����F�ڱ�AB�ϣ�����CF���߶�BE�ڵ�G��CG2=GEGD�� 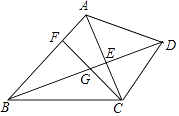
��1����֤����ACF=��ABD��
��2������EF����֤��EFCG=EGCB��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com