
����Ŀ��ij��������ˮ�����������£�ԭʼ��ˮ���Ⱦ���Aϵͳ���������������ˮ��A��ˮ���ﵽ����������ƴ�꣩�ĸ���Ϊp��0��p��1�����������⣬��ȷ�ϴ����ֱ���ŷţ����������������Bϵͳ������ֱ���ŷţ� ij������4����ˮ����A��ˮ�أ��ֱ�ȡ������⣮�����ˮ�������ʱ���ȿ���������飬Ҳ���Խ����ɸ����������һ���飮���������ֻҪ����������꣬���������Ļ������ز���꣮�������������꣬������и�������������������飻�����������꣬��ԭˮ�ص���ˮֱ���ŷţ�
�����������ַ�����
����һ��������飻
��������ƽ���ֳ����黯�飻
��������������������һ���飬ʣ�µ�һ���������飻
�����ģ�����һ���飮
�������������ֵԽС������Խ���š���
���� �� ![]() ����2��A��ˮ������ϻ����������ĸ��ʣ�
����2��A��ˮ������ϻ����������ĸ��ʣ�
���� �� ![]() ������4��A��ˮ������Ҫ���飬���ʣ�����һ�����������ĸ���š���
������4��A��ˮ������Ҫ���飬���ʣ�����һ�����������ĸ���š���
���� �������������ȡ������ġ������š�����p��ȡֵ��Χ��
���𰸡��⣺����2��A������������ĸ����� ![]() ���� ���Ը��ݶ����¼�ԭ����2��A��������������ĸ���Ϊ
���� ���Ը��ݶ����¼�ԭ����2��A��������������ĸ���Ϊ ![]() ����
����
��II������һ�������⣬������Ϊ��=4��
���������ɣ�I��֪��ÿ��2�������ļ��ʱ��������������Ϊ1������Ϊ ![]() ��
��
��������������Ϊ3������Ϊ ![]() ��
��
�ʷ������ļ�����Ϊ��2 �� ���2����ȡֵΪ2��4��6��
����ʷֲ������£�
��2 | 2 | 4 | 6 |
P | | | |
����÷�����������Ϊ ![]() ����
����
�����ģ�����һ���⣬�Ǽ�����Ϊ��4 ��
���4��ȡֵΪ1��5������ʷֲ������£�
��4 | 1 | 5 |
P | | |
����÷����ĵ�����Ϊ ![]() ����
����
�ȽϿɵ�E����4����E����2����4����ѡ������š�����
��III�����������軯�����Ϊ��3 �� ���3��ȡֵΪ2��5��
����ʷֲ�Ϊ��
��3 | 2 | 5 |
P | p3 | 1��p3 |
��ѧ����Ϊ ![]() ����
����
�����ģ��軯�����Ϊ��4 �� ���4��ȡֵΪ1��5��
����ʷֲ�Ϊ��
��4 | 1 | 5 |
P | p4 | 1��p4 |
��ѧ����Ϊ ![]() ����
����
�������E����3����E����4��������5��3p3��5��4p4 �� ���p�� ![]() ��
��
���Ե� ![]() ʱ���������ȷ����ĸ����š�
ʱ���������ȷ����ĸ����š�
��������������2��A������������ĸ��ʣ��ٸ��ݶ����¼�ԭ��������Dz����ĸ��ʣ���II�����㷽��һ�������⣬������Ϊ��=4�� ��������������Ϊ��2 �� ���2����ȡֵΪ2��4��6������ʷֲ��У�������ѧ������
�����ģ�����һ���⣬������Ϊ��4 �� ���4��ȡֵΪ1��5������ʷֲ��У�������ѧ������
�Ƚϵó�ѡ������š�����III�����������������Ϊ��3 �� ���3��ȡֵΪ2��5������ʷֲ��У�������ѧ������
�����ģ��������Ϊ��4 �� ���4��ȡֵΪ1��5������ʷֲ���������ѧ������
�������в���ʽE����3����E����4�������p��ȡֵ��Χ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ�ƻ��ٿ��������������С�������������Ҫѡ�λ�����ˣ�����ȫУѧ��ͶƱ�Ƽ�����2��������1��Ů�����Ƽ�Ϊ��ѡ�����ˣ�
��1��С����Ϊ�������3����ѡ�����������ѡ��1�������ˣ�������������Ů�������ѡ������������������Ů���Ŀ�������ͬ����ͬ������˵����Ϊʲô��
��2�������3����ѡ�����������ѡ��2�������ˣ���ͨ���б�����״ͼ��ѡ�γ���2��������ǡ����1��������1��Ů���ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ŀڴ���װ��4���ֱ�������֩�1����2��3��4��С�����ǵ���״����С��ȫ��ͬ��С���ȴӿڴ����������һ��С���������Ϊx��Сӱ��ʣ�µ�3��С�����������һ��С���������Ϊy��
��1��С��������������3��С��ĸ�����___��
��2�������б�������״ͼ�ķ�����ʾ����x��yȷ���ĵ�P��x��y�����п��ܵĽ����
��3�����涨����P��x��y���ڵ�һ�����������С���ʤ����P��x��y���ڵڶ��������������Сӱ��ʤ����ֱ�������˻�ʤ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����PAD�͵���ABCD������ABCD��ƽ���ı��Σ���ABC=45�㣬AD=AP=2��AB=DP=2 ![]() ��EΪCD���е㣬��F���߶�PB�ϣ�
��EΪCD���е㣬��F���߶�PB�ϣ� 
������֤��AD��PC��
��������B��EFC�������������P��ABCD����� ![]() ʱ����
ʱ���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������P��ABCD�ĵ��治��ƽ���ı��Σ���ƽ�� ��ȥ�ش�������ʹ�ý����ı�����ƽ���ı��Σ���������ƽ����� �� 
A.������
B.ֻ��1��
C.ǡ��4��
D.���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=|x��a|+| ![]() x+1|����СֵΪ2�� ������ʵ��a��ֵ��
x+1|����СֵΪ2�� ������ʵ��a��ֵ��
������a��0����ʽf��x����4�Ľ⼯��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪a��b��c�ֱ�Ϊ��ABC���ڽ�A��B��C�ĶԱߣ�btanA=2asinB��
��1����A��
��2����a= ![]() ��2b��c=4�����ABC�������
��2b��c=4�����ABC�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���ACB=90�㣬AB=9��cosB= ![]() ���ѡ�ABC���ŵ�C��ת��ʹ��B��AB���ϵĵ�D�غϣ���A���ڵ�E�����A��E֮��ľ���Ϊ ��
���ѡ�ABC���ŵ�C��ת��ʹ��B��AB���ϵĵ�D�غϣ���A���ڵ�E�����A��E֮��ľ���Ϊ �� 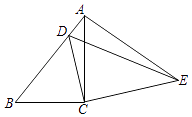
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=AC������A��AD��BC������Ϊ��D���ӳ�AD����E��ʹDE= ![]() AD������A��AF��BC����EC���ӳ����ڵ�F��
AD������A��AF��BC����EC���ӳ����ڵ�F�� 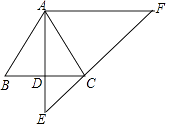
��1���� ![]() =
= ![]() ��
�� ![]() =
= ![]() ����
���� ![]() ��
�� ![]() ��������ϱ�ʾ
��������ϱ�ʾ ![]() ��
��
��2���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com