
【题目】已知a、b、c分别为△ABC的内角A、B、C的对边,btanA=2asinB.
(1)求A;
(2)若a= ![]() ,2b﹣c=4,求△ABC的面积.
,2b﹣c=4,求△ABC的面积.
【答案】
(1)解:∵btanA=2asinB.
∴ ![]() ,
,
又∵ ![]() ,
,
∴sinA= ![]() =
= ![]() ,
,
∵A∈(0,π),sinA≠0,
∴解得:cosA= ![]() ,
,
∴A= ![]() .
.
(2)解:∵A= ![]() ,a=
,a= ![]() ,
,
∴由余弦定理可得:7=b2+c2﹣bc,①
又∵2b﹣c=4,②
∴联立①②解得: ![]() 或
或 ![]() (舍去),
(舍去),
∴S△ABC= ![]() bcsinA=
bcsinA= ![]() =
= ![]() .
.
【解析】(1)由已知利用正弦定理化简可求sinA= ![]() ,结合sinA≠0,解得:cosA=
,结合sinA≠0,解得:cosA= ![]() ,即可得解A的值.(2)由余弦定理可得7=b2+c2﹣bc,又2b﹣c=4,联立解得b,c的值,利用三角形面积公式即可计算得解.
,即可得解A的值.(2)由余弦定理可得7=b2+c2﹣bc,又2b﹣c=4,联立解得b,c的值,利用三角形面积公式即可计算得解.
【考点精析】根据题目的已知条件,利用正弦定理的定义的相关知识可以得到问题的答案,需要掌握正弦定理:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某中学要进行理、化实验加试,需用九年级两个班级的学生整理实验器材.已知一班单独整理需要30分钟完成.
(1)如果一班与二班共同整理15分钟后,一班另有任务需要离开,剩余工作由二班单独整理15分钟才完成任务,求二班单独整理这批实验器材需要多少分钟?
(2)如果一、二的工作效率不变,先由二班单独整理,时间不超过20分钟,剩余工作再由一班独立完成,那么整理完这批器材一班至少还需要多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,点D,E,F分别在AB,BC,AC上,且∠ADF+∠DEC=180°,∠AFE=∠BDE.
(1)如图1,当DE=DF时,图1中是否存在与AB相等的线段?若存在,请找出,并加以证明;若不存在,说明理由;
(2)如图2,当DE=kDF(其中0<k<1)时,若∠A=90°,AF=m,求BD的长(用含k,m的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂的污水处理程序如下:原始污水必先经过A系统处理,处理后的污水(A级水)达到环保标准(简称达标)的概率为p(0<p<1).经化验检测,若确认达标便可直接排放;若不达标则必须进行B系统处理后直接排放. 某厂现有4个标准水量的A级水池,分别取样、检测.多个污水样本检测时,既可以逐个化验,也可以将若干个样本混合在一起化验.混合样本中只要有样本不达标,则混合样本的化验结果必不达标.若混合样本不达标,则该组中各个样本必须再逐个化验;若混合样本达标,则原水池的污水直接排放.
现有以下四种方案,
方案一:逐个化验;
方案二:平均分成两组化验;
方案三:三个样本混在一起化验,剩下的一个单独化验;
方案四:混在一起化验.
化验次数的期望值越小,则方案的越“优”.
(Ⅰ) 若 ![]() ,求2个A级水样本混合化验结果不达标的概率;
,求2个A级水样本混合化验结果不达标的概率;
(Ⅱ) 若 ![]() ,现有4个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
,现有4个A级水样本需要化验,请问:方案一,二,四中哪个最“优”?
(Ⅲ) 若“方案三”比“方案四”更“优”,求p的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( ) 
A.129
B.144
C.258
D.289
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的方程为 ![]() .以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2﹣8ρsinθ+15=0. (Ⅰ)写出C1的参数方程和C2的直角坐标方程;
.以坐标原点为极点,以x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2﹣8ρsinθ+15=0. (Ⅰ)写出C1的参数方程和C2的直角坐标方程;
(Ⅱ)设点P在C1上,点Q在C2上,求|PQ|的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC各顶点的坐标分别是A(﹣2,﹣4),B(0,﹣4),C(1,﹣1). 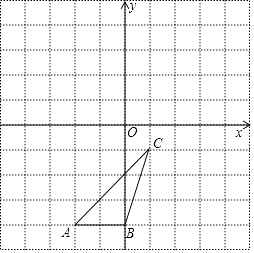
(1)在图中画出△ABC关于原点对称的△AB1C1;
(2)在图中画出△ABC绕原点C逆时针旋转90°后的△A2B2C2;
(3)在(2)的条件下,AC边扫过的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,AB∥CD,对角线AC、BD交于点E,点F在边AB上,连接CF交线段BE于点G,CG2=GEGD. 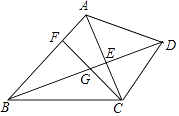
(1)求证:∠ACF=∠ABD;
(2)连接EF,求证:EFCG=EGCB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ![]() ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
(1)求AF和OF的长;
(2)如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com