
【题目】已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ![]() ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
(1)求AF和OF的长;
(2)如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.
【答案】
(1)
解:如图①
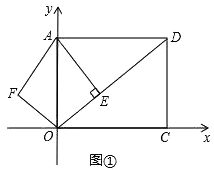
∵OA=5,AD=OC= ![]() ,
,
由勾股定理可求.OD= ![]() ,
,
∵AE×OD=AO×AD,
∴AE=4,
∴OE= ![]() =3,
=3,
∵点F是点E关于y轴的对称点,
∴AF=AE=4,OF=OE=3;
(2)
解:如图②
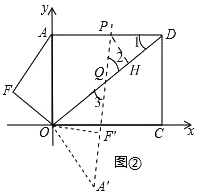
若PD=PQ,
易得∠1=∠2=∠3,
∵∠1=∠A′,
∴∠3=∠A′,
∴OQ=OA′=5,
∴DQ= ![]() ,
,
过点P作PH⊥DQ,
∴ ![]() ,
,
∵cos∠1= ![]() ,
,
∴DP= ![]() ,
,
∴AP= ![]() ,
,
∴此时点P的坐标为( ![]() ,5);
,5);
如图③
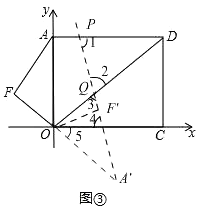
∵点P在线段AD上,
∴∠1>∠PDQ,
∴QP,QD不会相等;
如图③,
若DP=DQ,
易得,∠1=∠2=∠3=∠4,
∵∠3=∠5+∠A′,∠A′=∠COD,
∴∠4=∠A′OQ,
∴A′Q=A′O=5,
∴F′Q=5﹣4=1,
∴OQ= ![]() ,
,
∴DP=DQ= ![]() ﹣
﹣ ![]() ,
,
∴AP=AD﹣DP= ![]() ﹣
﹣ ![]() ,
,
∴此时点P的坐标为:( ![]() ﹣
﹣ ![]() ,5)
,5)
【解析】(1)运用勾股定理和面积相等法结合轴对称性质即可求解;(2)画出图形,根据PQ=PD,PD=DQ结合平行线的性质,对顶角相等和角的等量代换,运用勾股定理即可求解.


科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE= ![]() AD,过点A作AF∥BC,交EC的延长线于点F.
AD,过点A作AF∥BC,交EC的延长线于点F. 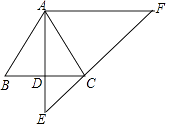
(1)设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,用
,用 ![]() 、
、 ![]() 的线性组合表示
的线性组合表示 ![]() ;
;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为 . 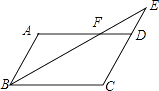
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:数学活动课上老师出示问题,如图1,有边长为a的正方形纸片一张,三边长分别为a、b、c的全等直角三角形纸片两张,且b ![]() .请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
.请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
解决问题: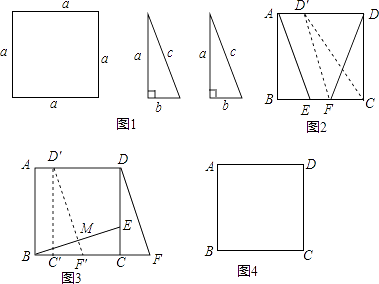
下面是两个学习小组拼出图案后提出的问题,请你解决他们提出的问题.
(1)“爱心”小组提出的问题是:如图2,将△DFC绕点F逆时针旋转,使点D恰好落在AD边上的点D′处,猜想此时四边形AEFD′是什么特殊四边形,并加以证明;
(2)“希望”小组提出的问题是:如图3,点M为BE中点,将△DCF向左平移至DF恰好过点M时停止,且补充条件a=6,b=2,求△DCF平移的距离.
自主创新:
(3)请你仿照上述小组的同学,在下面图4的空白处用实线画出你拼出的图案,用虚线画出变换图,并在横线处写出你提出的问题.(不必解答)
你提出的问题: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1 , 作第二个正方形A1B1C1C;延长C1B1交x轴于点A2 , 作第三个正方形A2B2C2C1 , …,按这样的规律进行下去,第2016个正方形的面积为( ) 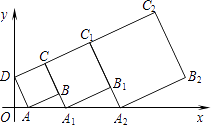
A.20×( ![]() )4030
)4030
B.20×( ![]() )4032
)4032
C.20×( ![]() )2016
)2016
D.20×( ![]() )2015
)2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是直线l上的两点,AB=4厘米,过l外一点C作CD∥l,射线BC与l所组成的锐角为60°,线段BC=2厘米,动点P、Q分别从B、C同时出发,P以1厘米/秒的速度,沿由B向C的方向运动;Q以2厘米/秒的速度,沿由C向D的方向运动,设P、Q运动的时间为t秒,当t>2时,PA交CD于点E. 
(1)用含t的代数式分别表示CE和QE的长;
(2)求△APQ的面积s与t的函数表达式;
(3)当QE恰好平分△APQ的面积时,QE的长是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com