
【题目】如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为 . 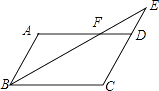
【答案】60
【解析】解:∵四边形ABCD是平行四边形, ∴AB=DC,AD∥BC,AB∥CD,
∵ED:DC=2:3,
∴ED:CE=2:5,ED:AB=2:3,
∵AD∥BC,AB∥CD,
∴△DEF∽△CEB,△DEF∽△ABF,
∴ ![]() =(
=( ![]() )2=(
)2=( ![]() )2=
)2= ![]() ,
, ![]() =(
=( ![]() )2=(
)2=( ![]() )2=
)2= ![]()
∵△DEF的面积为8,
∴△CEB的面积为50,△ABF的面积为18,
∴四边形DFBC的面积为50﹣8=42,
∴平行四边形ABCD的面积为42+18=60,
所以答案是:60.
【考点精析】认真审题,首先需要了解平行四边形的性质(平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分),还要掌握相似三角形的判定与性质(相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方)的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法至今仍是比较先进的算法.如图的程序框图是针对某一多项式求值的算法,如果输入的x的值为2,则输出的v的值为( ) 
A.129
B.144
C.258
D.289
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,∠BAD=∠CDA,AB=DC= ![]() ,CE=a,AC=b,求证:
,CE=a,AC=b,求证: 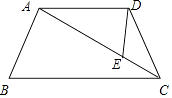
(1)△DEC∽△ADC;
(2)AEAB=BCDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.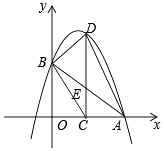
(1)求证:△BDE∽△CAE;
(2)已知OC=2,tan∠DAC=3,求此抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图①,在平面直角坐标系xOy中,A(0,5),C( ![]() ,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
,0),AOCD为矩形,AE垂直于对角线OD于E,点F是点E关于y轴的对称点,连AF、OF.
(1)求AF和OF的长;
(2)如图②,将△OAF绕点O顺时针旋转一个角α(0°<α<180°),记旋转中的△OAF为△OA′F′,在旋转过程中,设A′F′所在的直线与线段AD交于点P,与线段OD交于点Q,是否存在这样的P、Q两点,使△DPQ为等腰三角形?若存在,求出此时点P坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与操作:我们在学习四边形的相关知识时,认识了平行四边形、矩形、菱形、正方形等一些特殊的四边形,下面我们用尺规作图的方法来体会它们之间的联系.如图,在ABCD中,AB=4,BC=6,∠ABC=60°,请完成下列任务: 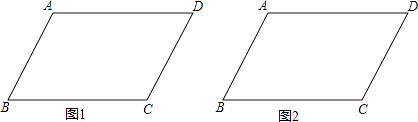
(1)在图1中作一个菱形,使得点A、B为所作菱形的2个顶点,另外2个顶点在ABCD的边上;在图2中作一个菱形,使点B、D为所作菱形的2个顶点,另外2个顶点在ABCD的边上;(尺规作图,保留作图痕迹,不写作法)
(2)请在图形下方横线处直接写出你按(1)中要求作出的菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径. 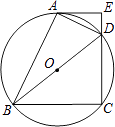
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一副扑克牌中取出的两组牌,分别是红桃1,2,3和方块1,2,3,将它们的背面朝上分别重新洗牌后,再从两组牌中各摸出一张. 
(1)用列表或树状图的方法表示此游戏所有可能出现的结果;
(2)求摸出的两张牌的牌面数字之和不小于4的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com