
【题目】如图,四边形ABCD 内接于⊙O,BD是⊙O的直径,过点A作⊙O的切线AE交CD的延长线于点E,DA平分∠BDE.
(1)求证:AE⊥CD;
(2)已知AE=4cm,CD=6cm,求⊙O的半径. 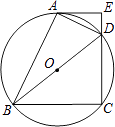
【答案】
(1)证明:连接OA.
∵AE是⊙O切线,
∴OA⊥AE,
∴∠OAE=90°,
∴∠EAD+∠OAD=90°,
∵∠ADO=∠ADE,OA=OD,
∴∠OAD=∠ODA=∠ADE,
∴∠EAD+∠ADE=90°,
∴∠AED=90°,
∴AE⊥CD;
(2)解:过点O作OF⊥CD,垂足为点F.
∵∠OAE=∠AED=∠OFD=90°,
∴四边形AOFE是矩形.
∴OF=AE=4cm.
又∵OF⊥CD,
∴DF= ![]() CD=3cm.
CD=3cm.
在Rt△ODF中,OD= ![]() =5cm,
=5cm,
即⊙O的半径为5cm.
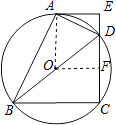
【解析】(1)欲证明AE⊥CD,只要证明∠EAD+∠ADE=90°即可;(2)过点O作OF⊥CD,垂足为点F.从而证得四边形AOFE是矩形,得出OF=AE,根据垂径定理得出DF= ![]() CD,在Rt△ODF中,根据勾股定理即可求得⊙O的半径.
CD,在Rt△ODF中,根据勾股定理即可求得⊙O的半径.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=3,BC=2,边AB的垂直平分线交AC边于点D,交AB边于点E,联结DB,那么tan∠DBC的值是 . 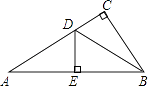
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为 . 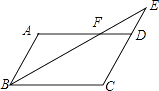
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:数学活动课上老师出示问题,如图1,有边长为a的正方形纸片一张,三边长分别为a、b、c的全等直角三角形纸片两张,且b ![]() .请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
.请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
解决问题: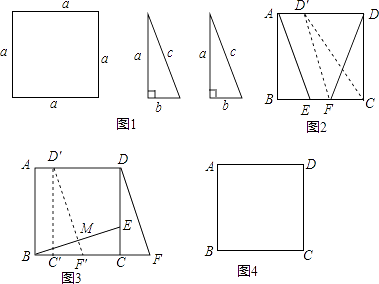
下面是两个学习小组拼出图案后提出的问题,请你解决他们提出的问题.
(1)“爱心”小组提出的问题是:如图2,将△DFC绕点F逆时针旋转,使点D恰好落在AD边上的点D′处,猜想此时四边形AEFD′是什么特殊四边形,并加以证明;
(2)“希望”小组提出的问题是:如图3,点M为BE中点,将△DCF向左平移至DF恰好过点M时停止,且补充条件a=6,b=2,求△DCF平移的距离.
自主创新:
(3)请你仿照上述小组的同学,在下面图4的空白处用实线画出你拼出的图案,用虚线画出变换图,并在横线处写出你提出的问题.(不必解答)
你提出的问题: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,第一个正方形ABCD的位置如图所示,点A的坐标为(2,0),点D的坐标为(0,4).延长CB交x轴于点A1 , 作第二个正方形A1B1C1C;延长C1B1交x轴于点A2 , 作第三个正方形A2B2C2C1 , …,按这样的规律进行下去,第2016个正方形的面积为( ) 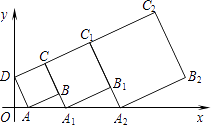
A.20×( ![]() )4030
)4030
B.20×( ![]() )4032
)4032
C.20×( ![]() )2016
)2016
D.20×( ![]() )2015
)2015
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,二次函数y=﹣x2+bx+c的图象与x轴交于A、B两点,与y轴交于C(0,3),A点在原点的左侧,B点的坐标为(3,0).点P是抛物线上一个动点,且在直线BC的上方.
(1)求这个二次函数的表达式.
(2)连接PO、PC,并把△POC沿CO翻折,得到四边形POP′C,那么是否存在点P,使四边形POP′C为菱形?若存在,请求出此时点P的坐标;若不存在,请说明理由.
(3)当点P运动到什么位置时,四边形 ABPC的面积最大,并求出此时点P的坐标和四边形ABPC的最大面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,天星山山脚下西端A处与东端B处相距800(1+ ![]() )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为 ![]() 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在北海市创建全国文明城活动中,需要20名志愿者担任“讲文明树新风”公益广告宣传工作,其中男生8人,女生12人.
(1)若从这20人中随机选取一人作为“展板挂图”讲解员,求选到女生的概率;
(2)若“广告策划”只在甲、乙两人中选一人,他们准备以游戏的方式决定由谁担任,游戏规则如下:将四张牌面数字分别为2,3,4,5的扑克牌洗匀后,数字朝下放于桌面,从中任取2张,若牌面数字之和为偶数,则甲担任,否则乙担任.试问这个游戏公平吗?请用树状图或列表法说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com