
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.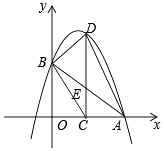
(1)求证:△BDE∽△CAE;
(2)已知OC=2,tan∠DAC=3,求此抛物线的表达式.
【答案】
(1)
证明:∵∠DCB=∠DAB,∠BEC=∠DEA,
∴△BEC∽△DEA,
∴ ![]() =
= ![]() ,又∠BED=∠CEA,
,又∠BED=∠CEA,
∴△BDE∽△CAE;
(2)
解:∵抛物线y=ax2+bx+4与y轴相交于点B,
∴点B的坐标为(0,4),即OB=4,
∵tan∠DAC=3,
∴ ![]() =3,
=3,
设AC=m,则DC=3m,OA=m+2,
则点A的坐标为(m+2,0),点D的坐标为(2,3m),
∵△BDE∽△CAE,
∴∠DBA=∠DCA=90°,
∴BD2+BC2=CD2,即22+(3m﹣4)2+(m+2)2+42=m2+(3m)2,
解得,m=2,
则点A的坐标为(4,0),点D的坐标为(2,6),
∴ ![]() ,
,
解得, ![]() ,
,
∴抛物线的表达式为y=﹣x2+3x+4
【解析】(1)根据相似三角形的判定定理得到△BEC∽△DEA,根据相似三角形的性质定理得到 ![]() =
= ![]() ,根据相似三角形的判定定理证明即可;(2)设AC=m,根据正切的定义得到DC=3m,根据相似三角形的性质得到∠DBA=∠DCA=90°,根据勾股定理列出算式,求出m的值,利用待定系数法求出抛物线的解析式.
,根据相似三角形的判定定理证明即可;(2)设AC=m,根据正切的定义得到DC=3m,根据相似三角形的性质得到∠DBA=∠DCA=90°,根据勾股定理列出算式,求出m的值,利用待定系数法求出抛物线的解析式.
【考点精析】根据题目的已知条件,利用二次函数的概念和二次函数的图象的相关知识可以得到问题的答案,需要掌握一般地,自变量x和因变量y之间存在如下关系:一般式:y=ax2+bx+c(a≠0,a、b、c为常数),则称y为x的二次函数;二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】设四棱锥P﹣ABCD的底面不是平行四边形,用平面 α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α( ) 
A.不存在
B.只有1个
C.恰有4个
D.有无数多个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=3,BC=2,边AB的垂直平分线交AC边于点D,交AB边于点E,联结DB,那么tan∠DBC的值是 . 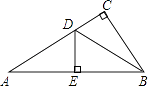
查看答案和解析>>
科目:初中数学 来源: 题型:
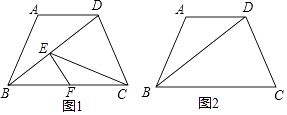
【题目】如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC= ![]() .点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=
.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y= ![]() .
.
(1)求BD的长;
(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;
(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,过点A作AD⊥BC,垂足为点D,延长AD至点E,使DE= ![]() AD,过点A作AF∥BC,交EC的延长线于点F.
AD,过点A作AF∥BC,交EC的延长线于点F. 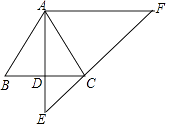
(1)设 ![]() =
= ![]() ,
, ![]() =
= ![]() ,用
,用 ![]() 、
、 ![]() 的线性组合表示
的线性组合表示 ![]() ;
;
(2)求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,若ED:DC=2:3,△DEF的面积为8,则平行四边形ABCD的面积为 . 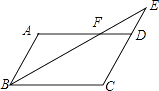
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景:数学活动课上老师出示问题,如图1,有边长为a的正方形纸片一张,三边长分别为a、b、c的全等直角三角形纸片两张,且b ![]() .请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
.请你用这三张纸片拼出一个图案,并将这个图案的某部分进行旋转或平移变换之后,提出一个问题(可以添加其他条件,例如可以给出a、b的值等等).
解决问题: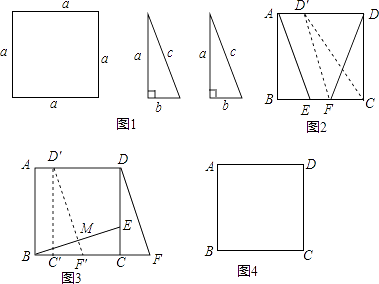
下面是两个学习小组拼出图案后提出的问题,请你解决他们提出的问题.
(1)“爱心”小组提出的问题是:如图2,将△DFC绕点F逆时针旋转,使点D恰好落在AD边上的点D′处,猜想此时四边形AEFD′是什么特殊四边形,并加以证明;
(2)“希望”小组提出的问题是:如图3,点M为BE中点,将△DCF向左平移至DF恰好过点M时停止,且补充条件a=6,b=2,求△DCF平移的距离.
自主创新:
(3)请你仿照上述小组的同学,在下面图4的空白处用实线画出你拼出的图案,用虚线画出变换图,并在横线处写出你提出的问题.(不必解答)
你提出的问题: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,天星山山脚下西端A处与东端B处相距800(1+ ![]() )米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为
)米,小军和小明同时分别从A处和B处向山顶C匀速行走.已知山的西端的坡角是45°,东端的坡角是30°,小军的行走速度为 ![]() 米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
米/秒.若小明与小军同时到达山顶C处,则小明的行走速度是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com