
【题目】如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC= ![]() .点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=
.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y= ![]() .
.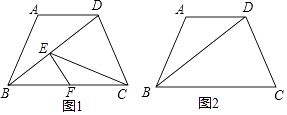
(1)求BD的长;
(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;
(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围.
【答案】
(1)
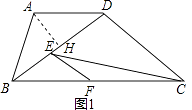
解:如图1,过A作AH⊥BD于H,
∵AD∥BC,AB=AD=5,
∴∠ABD=∠ADB=∠DBC,BH=HD,
在Rt△ABH中,
∵tan∠ABD=tan∠DBC= ![]() ,
,
∴cos∠ABD= ![]() ,
,
∴BH=DH=4,
∴BD=8;
(2)
解:∵△DCE是等腰三角形,且BC=BD=8,
∴①如图2,
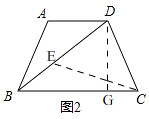
当CD=DE时,即:CD=DE=BD﹣BE=8﹣x,
过点D作DG⊥BC于G,
在Rt△BDG中,tan∠DBC= ![]() ,BD=8,
,BD=8,
∴DG= ![]() BD=
BD= ![]() ,BG=
,BG= ![]() BD=
BD= ![]() ,
,
∴CG=8﹣BG= ![]() ,
,
在Rt△CDG中,根据勾股定理得,DG2+CG2=CD2,
∴( ![]() )2+(
)2+( ![]() )2=(8﹣x)2,
)2=(8﹣x)2,
∴x=8+ ![]() (舍)或x=8﹣
(舍)或x=8﹣ ![]() ,
,
②如图3,
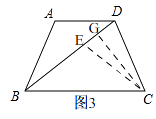
当CE=CD时,
过点C作CG⊥BD,
∴DG=EG= ![]() DE,
DE,
在Rt△BCG中,BC=8,tan∠DBC= ![]() ,
,
∴BG= ![]() ,
,
∴DG=BD﹣BG= ![]() ,
,
∴x=BE=BD﹣DE=BD﹣2DG= ![]()
(3)
解:∵BF=x,BC=10,
∴FC=10﹣x,
∴ ![]() ,
,
∵EF∥DC,
∴△FEB∽△CDB,
∴ ![]()
∴ ![]() =
= ![]() =﹣
=﹣ ![]() x2+
x2+ ![]() x(0<x<8)
x(0<x<8)
【解析】(1)过A作AH⊥BD于H,再根据AD∥BC,AB=AD=5,可得∠ABD=∠ADB=∠DBC,BH=HD,再根据tan∠ABD=tan ![]() ,计算出BH=DH=4,进而得到BD=8;(2)分两种情况用锐角三角函数计算即可得出结论.(3)首先利用平行线的性质得出△FEB∽△CDB,即可得出y与x的函数关系式;
,计算出BH=DH=4,进而得到BD=8;(2)分两种情况用锐角三角函数计算即可得出结论.(3)首先利用平行线的性质得出△FEB∽△CDB,即可得出y与x的函数关系式;
【考点精析】通过灵活运用梯形的定义和直角梯形,掌握一组对边平行,另一组对边不平行的四边形是梯形.两腰相等的梯形是等腰梯形;一腰垂直于底的梯形是直角梯形即可以解答此题.


科目:初中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2+ax2+bx﹣
x2+ax2+bx﹣ ![]() (a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|=
(a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|= ![]() ,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
(Ⅱ)证明关于x的方程(k2+1)ex﹣1﹣kf′(x)=0至多只有两个实数根(其中f′(x)是f(x)的导函数,e是自然对数的底数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大型购物商场在一楼和二楼之间安装自动扶梯AC,截面如图所示,一楼和二楼地面平行(即AB所在的直线与CD平行),层高AD为8米,∠ACD=20°,为使得顾客乘坐自动扶梯时不至于碰头,A、B之间必须达到一定的距离. (参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36)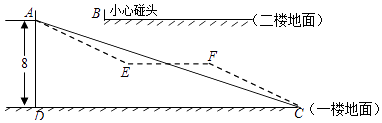
(1)要使身高2.26米的姚明乘坐自动扶梯时不碰头,那么A,B之间的距离至少要多少米?(精确到0.1米)
(2)如果自动扶梯改为由AE,EF,FC三段组成(如图中虚线所示),中间段EF为平台(即EF∥DC),AE段和FC段的坡度i=1:2,求平台EF的长度.(精确到0.1米)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在四边形ABCD中,∠BAD=∠CDA,AB=DC= ![]() ,CE=a,AC=b,求证:
,CE=a,AC=b,求证: 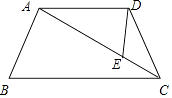
(1)△DEC∽△ADC;
(2)AEAB=BCDE.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,设 ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 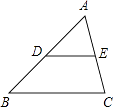
(1)求向量 ![]() (用向量
(用向量 ![]() ,
, ![]() 的式子表示).
的式子表示).
(2)在图中作出向量 ![]() 在向量
在向量 ![]() ,
, ![]() 方向上的分向量(不要求写作法,但要指出所作图中表示结论的向量).
方向上的分向量(不要求写作法,但要指出所作图中表示结论的向量).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=ax2+bx+4与x轴的正半轴相交于点A,与y轴相交于点B,点C在线段OA上,点D在此抛物线上,CD⊥x轴,且∠DCB=∠DAB,AB与CD相交于点E.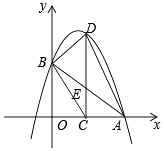
(1)求证:△BDE∽△CAE;
(2)已知OC=2,tan∠DAC=3,求此抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】实践与操作:我们在学习四边形的相关知识时,认识了平行四边形、矩形、菱形、正方形等一些特殊的四边形,下面我们用尺规作图的方法来体会它们之间的联系.如图,在ABCD中,AB=4,BC=6,∠ABC=60°,请完成下列任务: 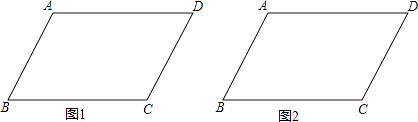
(1)在图1中作一个菱形,使得点A、B为所作菱形的2个顶点,另外2个顶点在ABCD的边上;在图2中作一个菱形,使点B、D为所作菱形的2个顶点,另外2个顶点在ABCD的边上;(尺规作图,保留作图痕迹,不写作法)
(2)请在图形下方横线处直接写出你按(1)中要求作出的菱形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=cm.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com