
����Ŀ��ʵ���������������ѧϰ�ı��ε����֪ʶʱ����ʶ��ƽ���ı��Ρ����Ρ����Ρ������ε�һЩ������ı��Σ����������ó߹���ͼ�ķ������������֮�����ϵ����ͼ����ABCD�У�AB=4��BC=6����ABC=60�㣬������������� 
��1����ͼ1����һ�����Σ�ʹ�õ�A��BΪ�������ε�2�����㣬����2��������ABCD�ı��ϣ���ͼ2����һ�����Σ�ʹ��B��DΪ�������ε�2�����㣬����2��������ABCD�ı��ϣ����߹���ͼ��������ͼ�ۼ�����д������
��2������ͼ���·����ߴ�ֱ��д���㰴��1����Ҫ�����������ε������
���𰸡�
��1���⣺��ͼ��ʾ��
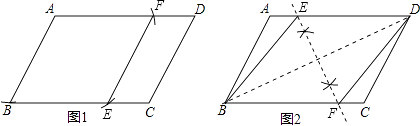
��2���⣺��ͼ1����ABCD�ĸ�AH��
��ֱ�ǡ�ABH�У���AB=4����ABC=60�㣬
��AH=ABsin60��=4�� ![]() =2
=2 ![]() ��BH=ABcos60��=4��
��BH=ABcos60��=4�� ![]() =2��
=2��
��S����ABEF=BEAH=4��2 ![]() =8
=8 ![]() ��
��
��ͼ2����BD��EF���ڵ�O����DM��BC��M����CM=BH=2��DM=AH=2 ![]() ��
��
��ֱ�ǡ�BDM�У��ߡ�M=90�㣬
��BD= ![]() =
= ![]() =2
=2 ![]() ��
��
��BF=x��CF=y����DF=x��
������� ![]() ��
��
��� 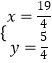 ��
��
��OF= ![]() =
= ![]() =
= ![]() ��
��
��S����ABEF= ![]() BDEF=
BDEF= ![]() ��2
��2 ![]() ��
�� ![]() =
= ![]() ��
��
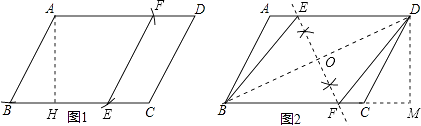
����������1����ͼ1����AD��BC�Ϸֱ��ȡAF=BE=4������EF�����ı���ABEF�����Σ���ͼ2������BD����BD�Ĵ�ֱƽ���ߣ���AD��E��BC��F�����ı���BEDF�����Σ���2����ͼ1����ABCD�ĸ�AH���������ε����=�ס�����ʽ���㼴�ɣ���ͼ2����BD��EF���ڵ�O����DM��BC��M����CM=BH=2��DM=AH=2 ![]() ���ֱ����BD��EF���������ε����=���Խ��߳˻���һ����ʽ���㼴�ɣ�
���ֱ����BD��EF���������ε����=���Խ��߳˻���һ����ʽ���㼴�ɣ�
�����㾫����������Ĺؼ���������ƽ���ı��ε����ʵ����֪ʶ������ƽ���ı��εĶԱ������ƽ�У�ƽ���ı��εĶԽ���ȣ��ڽǻ�����ƽ���ı��εĶԽ�����ƽ�֣��Լ������ε����ʵ����⣬�˽����ε������߶���ȣ����εĶԽ����ഹֱ������ÿһ���Խ���ƽ��һ��Խǣ����α������Խ��߷ֳ��ĸ�ȫ�ȵ�ֱ�������Σ����ε�������������Խ��߳��Ļ���һ�룮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУ���꼶��ѧģ������У�����ѧ������ѧ�ɼ����£���λ���֣���110��106��109��111��108��110�����й�����������������ȷ���ǣ� ��
A.������110
B.������16
C.ƽ������109.5
D.������6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������ABCD�У�AD��BC��AB=AD=5��tan��DBC= ![]() ����EΪ�߶�BD������һ�㣨��E���B��D���غϣ�������E��EF��CD����BC�ཻ�ڵ�F������CE����BE=x��y=
����EΪ�߶�BD������һ�㣨��E���B��D���غϣ�������E��EF��CD����BC�ཻ�ڵ�F������CE����BE=x��y= ![]() ��
��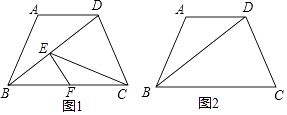
��1����BD�ij���
��2�����BC=BD������DCE�ǵ���������ʱ����x��ֵ��
��3�����BC=10����y����x�ĺ�������ʽ����д���Ա���x��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�E��CD���ӳ�����һ�㣬BE��AD���ڵ�F����ED��DC=2��3����DEF�����Ϊ8����ƽ���ı���ABCD�����Ϊ �� 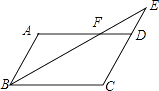
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ҹ��Ŵ��伮��ׯ������ƪ������˵��һ�仰����һ��֮颣���ȡ��룬�������ߡ�������һ����Ϊ1�ߵ�ľ�ˣ���1�ν�ȡ�䳤�ȵ�һ�룬��2�ν�ȡ���1��ʣ�³��ȵ�һ�룬��3�ν�ȡ���2��ʣ�³��ȵ�һ�룬��˷��������99�ν�ȡ��ľ��ʣ�µij���Ϊ�� ��
A.![]() ��
��
B.![]() ��
��
C.![]() ��
��
D.![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ������ѧ�������ʦ��ʾ���⣬��ͼ1���б߳�Ϊa��������ֽƬһ�ţ����߳��ֱ�Ϊa��b��c��ȫ��ֱ��������ֽƬ���ţ���b ![]() ��������������ֽƬƴ��һ��ͼ�����������ͼ����ij���ֽ�����ת��ƽ�Ʊ任֮�����һ�����⣨������������������������Ը���a��b��ֵ�ȵȣ���
��������������ֽƬƴ��һ��ͼ�����������ͼ����ij���ֽ�����ת��ƽ�Ʊ任֮�����һ�����⣨������������������������Ը���a��b��ֵ�ȵȣ���
������⣺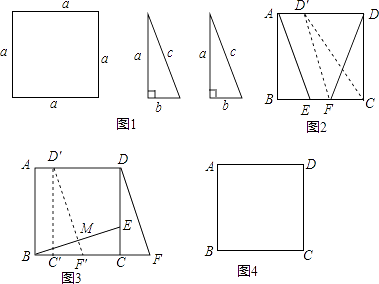
����������ѧϰС��ƴ��ͼ������������⣬������������������⣮
��1�������ġ�С������������ǣ���ͼ2������DFC�Ƶ�F��ʱ����ת��ʹ��Dǡ������AD���ϵĵ�D�䴦�������ʱ�ı���AEFD����ʲô�����ı��Σ�������֤����
��2����ϣ����С������������ǣ���ͼ3����MΪBE�е㣬����DCF����ƽ����DFǡ�ù���Mʱֹͣ���Ҳ�������a=6��b=2�����DCFƽ�Ƶľ��룮
�������£�
��3�������������С���ͬѧ��������ͼ4�Ŀհ״���ʵ������ƴ����ͼ�������������任ͼ�����ں��ߴ�д������������⣮�����ؽ��
����������⣺ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������
��1�����㣺�� ![]() ��0+
��0+ ![]() ��|��3|+tan45�㣻
��|��3|+tan45�㣻
��2�����㣺��x+2��2��2��x��1����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У����κ���y=��x2+bx+c��ͼ����x�ύ��A��B���㣬��y�ύ��C��0��3����A����ԭ�����࣬B�������Ϊ��3��0������P����������һ�����㣬����ֱ��BC���Ϸ���
��1����������κ����ı���ʽ��
��2������PO��PC�����ѡ�POC��CO���ۣ��õ��ı���POP��C����ô�Ƿ���ڵ�P��ʹ�ı���POP��CΪ���Σ������ڣ��������ʱ��P�����ꣻ�������ڣ���˵�����ɣ�
��3������P�˶���ʲôλ��ʱ���ı��� ABPC�������������ʱ��P��������ı���ABPC����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���OABC�Ǿ��Σ�ADEF�������Σ���A��D��x����������ϣ���C��y����������ϣ���F��AB�ϣ���B��E�ڷ���������y= ![]() ��ͼ���ϣ�OA=1��OC=6�������������ADEF�ı߳���
��ͼ���ϣ�OA=1��OC=6�������������ADEF�ı߳��� 
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com