
【题目】已知函数f(x)= ![]() x2+ax2+bx﹣
x2+ax2+bx﹣ ![]() (a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|=
(a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|= ![]() ,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
(Ⅱ)证明关于x的方程(k2+1)ex﹣1﹣kf′(x)=0至多只有两个实数根(其中f′(x)是f(x)的导函数,e是自然对数的底数)
【答案】解:(Ⅰ)求导f′(x)=x2+2ax+b,由f(x)在x=x1和x=x2处取得极值, 则x1 , x2是方程x2+2ax+b=0的两个根,则x1+x2=﹣2a,x1x2=b,
由|x1﹣x2|= ![]() ,则(x1+x2)2﹣4x1x2=5,则4a2﹣4b=5,①
,则(x1+x2)2﹣4x1x2=5,则4a2﹣4b=5,①
由曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直,
则f′(1)=1,
即2a+b+1=0,②,
解得: 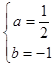 .
.
∴f(x)= ![]() x3+
x3+ ![]() x2﹣x﹣
x2﹣x﹣ ![]() ,
,
(Ⅱ)对于(k2+1)ex﹣1﹣kf′(x)=0,
当k=0时,ex﹣1=0,方程为实根,
当k≠0时,k+ ![]() =
= ![]() ,令g(x)=
,令g(x)= ![]() ,
,
g′(x)=﹣e ![]() =﹣e
=﹣e ![]() ,
,
当x∈(﹣∞,﹣1)∪(2,+∞)时,g′(x)<0,
∴g(x)的单调递减区间(﹣∞,﹣1),(2,+∞)单调递增区间(﹣1,2),
函数g(x)在x=﹣1和x=2处分别求得极小值和极大值,
g(x)极小=g(﹣1)=﹣e2<0,g(x)极大=g(2)= ![]() >0,
>0,
∴对于g(x)= ![]() ,由ex﹣1>0恒成立,
,由ex﹣1>0恒成立,
且y=x2+x﹣1时与x轴有两个交点,
从而g(x)无极大值,g(x)min=g(x)极小=g(﹣1)=﹣e2 ,
当k<0时,k+ ![]() ≤﹣2直线y=k+
≤﹣2直线y=k+ ![]() ,与曲线y=g(x)至多有两个交点,
,与曲线y=g(x)至多有两个交点,
当k>0时,k+ ![]() ≥2>
≥2> ![]() =g(x)极大 , 直线y=k+
=g(x)极大 , 直线y=k+ ![]() ,与曲线y=g(x)只有一个交点,
,与曲线y=g(x)只有一个交点,
∴方程(k2+1)ex﹣1﹣kf′(x)=0至多只有两个实数根.
【解析】(Ⅰ)由题意可知x1 , x2是方程x2+2ax+b=0的两个根,利用韦达定理及|x1﹣x2|= ![]() ,求得4a2﹣4b=5,由f′(1)=1,2a+b+1=0联立即可求得a和b的值,求得f(x)的解析式;(Ⅱ)由题意可知当k≠0时,k+
,求得4a2﹣4b=5,由f′(1)=1,2a+b+1=0联立即可求得a和b的值,求得f(x)的解析式;(Ⅱ)由题意可知当k≠0时,k+ ![]() =
= ![]() ,构造辅助函数,求导根据函数的单调性求得函数的极值及最值,利用基本不等式的性质,当k<0时,k+
,构造辅助函数,求导根据函数的单调性求得函数的极值及最值,利用基本不等式的性质,当k<0时,k+ ![]() ≤﹣2直线y=k+
≤﹣2直线y=k+ ![]() ,与曲线y=g(x)至多有两个交点,当k>0时,k+
,与曲线y=g(x)至多有两个交点,当k>0时,k+ ![]() ≥2>
≥2> ![]() =g(x)极大 , 直线y=k+
=g(x)极大 , 直线y=k+ ![]() ,与曲线y=g(x)只有一个交点,即可求证方程至多有两个实根.
,与曲线y=g(x)只有一个交点,即可求证方程至多有两个实根.
【考点精析】解答此题的关键在于理解函数的极值与导数的相关知识,掌握求函数![]() 的极值的方法是:(1)如果在
的极值的方法是:(1)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极大值(2)如果在
是极大值(2)如果在![]() 附近的左侧
附近的左侧![]() ,右侧
,右侧![]() ,那么
,那么![]() 是极小值.
是极小值.


科目:初中数学 来源: 题型:
【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计,结果保留根号形式)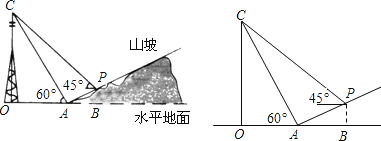
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】电视节目“奔跑吧兄弟”播出后深受中小学生的喜爱,小刚想知道大家最喜欢哪位“兄弟”,于是在本校随机抽取了一部分学生进行抽查(每人只能选一个自己最喜欢的“兄弟”),将调查结果进行了整理后绘制成如图两幅不完整的统计图,请结合图中提供的信息解答下列问题:
(1)本次被调查的学生有 人.
(2)将两幅统计图补充完整.
(3)若小刚所在学校有2000名学生,请根据图中信息,估计全校喜欢“Angelababy”的人数.
(4)若从3名喜欢“李晨”的学生和2名喜欢“Angelababy”的学生中随机抽取两人参加文体活动,则两人都是喜欢“李晨”的学生的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区共有1800名初三学生,为了解这些学生的体质健康状况,开学之初随机选取部分学生进行体育测试,以下是根据测试成绩绘制的统计图表的一部分.
等级 | 测试成绩(分) | 人数 |
优秀 | 45≤x≤50 | 140 |
良好 | 37.5≤x<45 | 36 |
及格 | 30≤x<37.5 | |
不及格 | x<30 | 6 |

根据以上信息,解答下列问题:
(1)本次测试学生体质健康成绩为良好的有人,达到优秀的人数占本次测试总人数的百分比为%.
(2)本次测试的学生数为人,其中,体质健康成绩为及格的有人,不及格的人数占本次测试总人数的百分比为%.
(3)试估计该地区初三学生开学之初体质健康成绩达到良好及以上等级的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知球O的半径为1,A,B是球面上的两点,且AB= ![]() ,若点P是球面上任意一点,则
,若点P是球面上任意一点,则 ![]()
![]() 的取值范围是( )
的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[0, ![]() ]
]
D.[0, ![]() ]
]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设四棱锥P﹣ABCD的底面不是平行四边形,用平面 α去截此四棱锥,使得截面四边形是平行四边形,则这样的平面α( ) 
A.不存在
B.只有1个
C.恰有4个
D.有无数多个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆M:(x﹣a)2+(y﹣b)2=9,M在抛物线C:x2=2py(p>0)上,圆M过原点且与C的准线相切. (Ⅰ)求C的方程;
(Ⅱ)点Q(0,﹣t)(t>0),点P(与Q不重合)在直线l:y=﹣t上运动,过点P作C的两条切线,切点分别为A,B.求证:∠AQO=∠BQO(其中O为坐标原点).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下(单位:分):110,106,109,111,108,110,下列关于这组数据描述正确的是( )
A.众数是110
B.方差是16
C.平均数是109.5
D.极差是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在梯形ABCD中,AD∥BC,AB=AD=5,tan∠DBC= ![]() .点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y=
.点E为线段BD上任意一点(点E与点B,D不重合),过点E作EF∥CD,与BC相交于点F,连接CE.设BE=x,y= ![]() .
.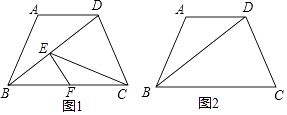
(1)求BD的长;
(2)如果BC=BD,当△DCE是等腰三角形时,求x的值;
(3)如果BC=10,求y关于x的函数解析式,并写出自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com