
【题目】已知球O的半径为1,A,B是球面上的两点,且AB= ![]() ,若点P是球面上任意一点,则
,若点P是球面上任意一点,则 ![]()
![]() 的取值范围是( )
的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[0, ![]() ]
]
D.[0, ![]() ]
]
【答案】B
【解析】解:∵OA=OB=1,AB= ![]() , ∴cos∠AOB=
, ∴cos∠AOB= ![]() =﹣
=﹣ ![]() ,即∠AOB=120°,
,即∠AOB=120°,
以球心O为原点,以平面AOB的垂线为竖轴建立空间坐标系,
设A(1,0,0),B(﹣ ![]() ,
, ![]() ,0),P(x,y,z)
,0),P(x,y,z)
则 ![]() =(1﹣x,﹣y,﹣z),
=(1﹣x,﹣y,﹣z), ![]() =(﹣
=(﹣ ![]() ﹣x,
﹣x, ![]() ﹣y,﹣z),且x2+y2+z2=1,
﹣y,﹣z),且x2+y2+z2=1,
∴ ![]() =(1﹣x)(﹣
=(1﹣x)(﹣ ![]() ﹣x)﹣y(
﹣x)﹣y( ![]() ﹣y)+z2=x2+y2+z2﹣
﹣y)+z2=x2+y2+z2﹣ ![]() (x+
(x+ ![]() y)﹣
y)﹣ ![]() =
= ![]() ﹣
﹣ ![]() (x+
(x+ ![]() y).
y).
∵P(x,y,z)是球上的一点,∴x2+y2≤1,
设m=x+ ![]() ,则当直线x+
,则当直线x+ ![]() y﹣m=0与圆x2+y2=1相切时,m取得最值,
y﹣m=0与圆x2+y2=1相切时,m取得最值,
∴ ![]() =1,∴﹣2≤m≤2,
=1,∴﹣2≤m≤2,
∴当m=﹣2时, ![]() 取得最大值
取得最大值 ![]() ,当m=2时,
,当m=2时, ![]() 取得最小值﹣
取得最小值﹣ ![]() .
.
故选B.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当 ![]() = 时,四边形ADFE是平行四边形.
= 时,四边形ADFE是平行四边形. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为( )
A.3
B.1.5
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,线段AB,CD表示甲、乙两幢居民楼的高,两楼间的距离BD是60米.某人站在A处测得C点的俯角为37°,D点的俯角为48°(人的身高忽略不计),求乙楼的高度CD.(参考数据:sin37°≈![]() ,tan37°≈
,tan37°≈![]() ,sin48°≈
,sin48°≈![]() ,tan48°≈
,tan48°≈![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,∠AOB=90°,AB∥x轴,OB=2,双曲线y=![]() 经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.
经过点B,将△AOB绕点B逆时针旋转,使点O的对应点D落在x轴的正半轴上.若AB的对应线段CB恰好经过点O.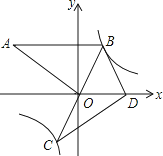
(1)求点B的坐标和双曲线的解析式;
(2)判断点C是否在双曲线上,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x2+ax2+bx﹣
x2+ax2+bx﹣ ![]() (a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|=
(a>0,b∈R),f(x)在x=x1和x=x2处取得极值,且|x1﹣x2|= ![]() ,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
,曲线y=f(x)在(1,f(1))处的切线与直线x+y=0垂直. (Ⅰ)求f(x)的解析式;
(Ⅱ)证明关于x的方程(k2+1)ex﹣1﹣kf′(x)=0至多只有两个实数根(其中f′(x)是f(x)的导函数,e是自然对数的底数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5支篮球队进行单循环比赛(任两支球队恰进行一场比赛),任两支球队之间胜率都是 ![]() .单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为
.单循环比赛结束,以获胜的场次数作为该队的成绩,成绩按从大到小排名次顺序,成绩相同则名次相同.有下列四个命题:p1:恰有四支球队并列第一名为不可能事件;p2:有可能出现恰有两支球队并列第一名;p3:每支球队都既有胜又有败的概率为 ![]() ;p4:五支球队成绩并列第一名的概率为
;p4:五支球队成绩并列第一名的概率为 ![]() .其中真命题是( )
.其中真命题是( )
A.p1 , p2 , p3
B.p1 , p2 , p4
C.p1 , p3 , p4
D.p2 , p3 , p4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选出建设方案A和B向社会公开征集意见.有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下: 
(Ⅰ)根据已知条件完成下面的2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关?
选择方案A | 选择方案B | 总计 | |
老年人 | |||
非老年人 | |||
总计 | 500 |
附:
(Ⅱ)根据(Ⅰ)的结论,能否提出一个更好的调查方法,使得调查结果更具代表性,说明理由.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E分别是边AB,AC的中点,设 ![]() =
= ![]() ,
, ![]() =
= ![]() .
. 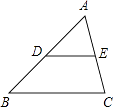
(1)求向量 ![]() (用向量
(用向量 ![]() ,
, ![]() 的式子表示).
的式子表示).
(2)在图中作出向量 ![]() 在向量
在向量 ![]() ,
, ![]() 方向上的分向量(不要求写作法,但要指出所作图中表示结论的向量).
方向上的分向量(不要求写作法,但要指出所作图中表示结论的向量).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com