
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD、等边△ABE,EF⊥AB,垂足为F,连接DF,当 ![]() = 时,四边形ADFE是平行四边形.
= 时,四边形ADFE是平行四边形. 
【答案】![]()
【解析】解:当 ![]() =
= ![]() 时,四边形ADFE是平行四边形.
时,四边形ADFE是平行四边形.
理由:∵ ![]() =
= ![]() ,
,
∴∠CAB=30°,
∵△ABE为等边三角形,EF⊥AB,
∴EF为∠BEA的平分线,∠AEB=60°,AE=AB,
∴∠FEA=30°,又∠BAC=30°,
∴∠FEA=∠BAC,
在△ABC和△EAF中,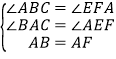
∴△ABC≌△EAF(AAS);
∵∠BAC=30°,∠DAC=60°,
∴∠DAB=90°,即DA⊥AB,
∵EF⊥AB,
∴AD∥EF,
∵△ABC≌△EAF,
∴EF=AC=AD,
∴四边形ADFE是平行四边形.
所以答案是: ![]() .
.
【考点精析】掌握等边三角形的性质和平行四边形的判定是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;两组对边分别平行的四边形是平行四边形:两组对边分别相等的四边形是平行四边形;一组对边平行且相等的四边形是平行四边形;两组对角分别相等的四边形是平行四边形;对角线互相平分的四边形是平行四边形.


科目:初中数学 来源: 题型:
【题目】为了解外来务工子女就学情况,某校对七年级各班级外来务工子女的人数情况进行了统计,发现各班级中外来务工子女的人数有1名、2名、3名、4名、5名、6名共六种情况,并制成如下两幅统计图: 
(1)求该校七年级平均每个班级有多少名外来务工子女?并将该条形统计图补充完整;
(2)学校决定从只有2名外来务工子女的这些班级中,任选两名进行生活资助,请用列表法或画树状图的方法,求出所选两名外来务工子女来自同一个班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC,OA=3,OC=6,将△ABC沿对角线AC翻折,使点B落在点B′处,AB′与y轴交于点D,则点D的坐标为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】菱形ABCD中,两条对角线AC,BD相交于点O,∠MON+∠BCD=180°,∠MON绕点O旋转,射线OM交边BC于点E,射线ON交边DC于点F,连接EF.
(1)如图1,当∠ABC=90°时,△OEF的形状是;
(2)如图2,当∠ABC=60°时,请判断△OEF的形状,并说明理由;
(3)在(1)的条件下,将∠MON的顶点移到AO的中点O′处,∠MO′N绕点O′旋转,仍满足∠MO′N+∠BCD=180°,射线O′M交直线BC于点E,射线O′N交直线CD于点F,当BC=4,且![]() =
=![]() 时,直接写出线段CE的长.
时,直接写出线段CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
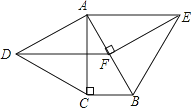
【题目】如图,某人在山坡坡脚A处测得电视塔尖点C的仰角为60°,沿山坡向上走到P处再测得点C的仰角为45°,已知OA=100米,山坡坡度(竖直高度与水平宽度的比)i=1:2,且O、A、B在同一条直线上.求电视塔OC的高度以及此人所在位置点P的铅直高度.(测倾器高度忽略不计,结果保留根号形式)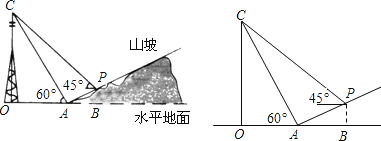
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,边长不等的正方形依次排列,每个正方形都有一个顶点落在函数![]() 的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则第4个正方形的边长是 , S3的值为 .
的图象上,从左向右第3个正方形中的一个顶点A的坐标为(6,2),阴影三角形部分的面积从左向右依次记为S1、S2、S3、…、Sn , 则第4个正方形的边长是 , S3的值为 . 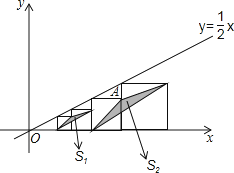
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明开了一家网店,进行社会实践,计划经销甲、乙两种商品.若甲商品每件利润10元,乙商品每件利润20元,则每周能卖出甲商品40件,乙商品20件.经调查,甲、乙两种商品零售单价分别每降价1元,这两种商品每周可各多销售10件.为了提高销售量,小明决定把甲、乙两种商品的零售单价都降价x元.
(1)直接写出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系式:y甲= , y乙=;
(2)求出小明每周销售甲、乙两种商品获得的总利润W(元)与降价x(元)之间的函数关系式?如果每周甲商品的销售量不低于乙商品的销售量的![]() ,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知球O的半径为1,A,B是球面上的两点,且AB= ![]() ,若点P是球面上任意一点,则
,若点P是球面上任意一点,则 ![]()
![]() 的取值范围是( )
的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[0, ![]() ]
]
D.[0, ![]() ]
]
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com