
【题目】为丰富人民群众业余生活,某市拟建设一座江滨公园,通过专家评审筛选出建设方案A和B向社会公开征集意见.有关部门用简单随机抽样方法调查了500名市民对这两种方案的看法,结果用条形图表示如下: 
(Ⅰ)根据已知条件完成下面的2×2列联表,并用独立性检验的方法分析,能否在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关?
选择方案A | 选择方案B | 总计 | |
老年人 | |||
非老年人 | |||
总计 | 500 |
附:
(Ⅱ)根据(Ⅰ)的结论,能否提出一个更好的调查方法,使得调查结果更具代表性,说明理由.
P(K2≥k) | 0.100 | 0.050 | 0.010 | 0.001 |
k | 2.706 | 3.841 | 6.635 | 10.828 |
![]() .
.
【答案】解:(Ⅰ)根据条形图填写2×2列联表如下,
选择方案A | 选择方案B | 总计 | |
老年人 | 20 | 180 | 200 |
非老年人 | 60 | 240 | 300 |
总计 | 80 | 420 | 500 |
计算观测值K2= ![]() ≈8.929>6.635,
≈8.929>6.635,
∴能在犯错误的概率不超过0.01的前提下认为是否选择方案A和年龄段有关;
(Ⅱ)根据(Ⅰ)的结论知人们是否选择方案A和B与年龄有关,
并且从样本中看出老年人与非老年人选择方案A和B的比例有明显差异,
因此在调查时可以先确定老年人与非老年人的比例,再利用分层抽样方法比简单随机抽样方法要好些.
【解析】(Ⅰ)根据条形图填写2×2列联表,计算观测值K2 , 比较临界值得出结论;(Ⅱ)根据(Ⅰ)的结论知人们是否选择方案A和B与是否为老年人有关, 抽样方法应考虑老年人与非老年人的比例,利用分层抽样要好些.


 特高级教师点拨系列答案
特高级教师点拨系列答案科目:初中数学 来源: 题型:
【题目】小明开了一家网店,进行社会实践,计划经销甲、乙两种商品.若甲商品每件利润10元,乙商品每件利润20元,则每周能卖出甲商品40件,乙商品20件.经调查,甲、乙两种商品零售单价分别每降价1元,这两种商品每周可各多销售10件.为了提高销售量,小明决定把甲、乙两种商品的零售单价都降价x元.
(1)直接写出甲、乙两种商品每周的销售量y(件)与降价x(元)之间的函数关系式:y甲= , y乙=;
(2)求出小明每周销售甲、乙两种商品获得的总利润W(元)与降价x(元)之间的函数关系式?如果每周甲商品的销售量不低于乙商品的销售量的![]() ,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
,那么当x定为多少元时,才能使小明每周销售甲、乙两种商品获得的总利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知球O的半径为1,A,B是球面上的两点,且AB= ![]() ,若点P是球面上任意一点,则
,若点P是球面上任意一点,则 ![]()
![]() 的取值范围是( )
的取值范围是( )
A.[ ![]() ,
, ![]() ]
]
B.[ ![]() ,
, ![]() ]
]
C.[0, ![]() ]
]
D.[0, ![]() ]
]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知圆M:(x﹣a)2+(y﹣b)2=9,M在抛物线C:x2=2py(p>0)上,圆M过原点且与C的准线相切. (Ⅰ)求C的方程;
(Ⅱ)点Q(0,﹣t)(t>0),点P(与Q不重合)在直线l:y=﹣t上运动,过点P作C的两条切线,切点分别为A,B.求证:∠AQO=∠BQO(其中O为坐标原点).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数f(x)= ![]() 若对于任意两个不等实数x1 , x2 , 都有
若对于任意两个不等实数x1 , x2 , 都有 ![]() >1成立,则实数a的取值范围是( )
>1成立,则实数a的取值范围是( )
A.[1,3)
B.[ ![]() ,3)
,3)
C.[0,4)
D.[ ![]() ,4)
,4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级数学模拟测试中,六名学生的数学成绩如下(单位:分):110,106,109,111,108,110,下列关于这组数据描述正确的是( )
A.众数是110
B.方差是16
C.平均数是109.5
D.极差是6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为6,E,F分别是AB,BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM. 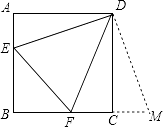
(1)求证:EF=FM.
(2)当AE=2时,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=﹣x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
从上表可知,下列说法中,错误的是( )
A.抛物线于x轴的一个交点坐标为(﹣2,0)
B.抛物线与y轴的交点坐标为(0,6)
C.抛物线的对称轴是直线x=0
D.抛物线在对称轴左侧部分是上升的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代典籍《庄子天下篇》中曾说过一句话:“一尺之棰,日取其半,万世不竭”,现有一根长为1尺的木杆,第1次截取其长度的一半,第2次截取其第1次剩下长度的一半,第3次截取其第2次剩下长度的一半,如此反复,则第99次截取后,此木杆剩下的长度为( )
A.![]() 尺
尺
B.![]() 尺
尺
C.![]() 尺
尺
D.![]() 尺
尺
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com